Comme l’expliquait si bien Dan Gardner dans son excellent livre Risk, l’humain est aveugle aux probabilités, c’est-à-dire que nous avons beaucoup de difficulté à évaluer les événements incertains. Les humains utilisent des raccourcis mentaux et des « règles du pouce » pour prendre des décisions plus rapidement, même si cela mène souvent à commettre des erreurs.
Le paradoxe de Monty Hall est une énigme soulevée par le statisticien américain Steve Selvin en 1975. Monty Hall était l’animateur de la populaire émission « Let’s Make a Deal », qui démarra aux États-Unis en 1963.
Supposons que Monty Hall vous place devant trois portes, derrière lesquelles il y a une voiture et deux chèvres. Si vous réussissez à deviner la porte derrière laquelle se cache la voiture, vous remportez ce prix.
- Il vous demande d’abord de choisir l’une des trois portes (supposons que vous choisissiez la porte numéro 1).
- Puis, Monty Hall ouvre l’une des deux autres portes derrière laquelle il sait qu’il y a une chèvre (disons la porte numéro 2).
- Finalement, il vous demande si vous désirez modifier votre choix.
Devriez-vous conserver votre choix ou changer pour la porte numéro 3 ?

Pensez-y quelques instants…
Il ne reste que deux portes… donc il y a une probabilité de 50% que la voiture soit derrière l’une ou l’autre, n’est-ce pas ? Conséquemment, vous devriez être indifférent entre la porte numéro 1 et la porte numéro 3… Vous décidez donc de ne pas changer votre choix…
Est-ce la bonne réponse ?
…
Non ! Votre cerveau a été déjoué ! Vous auriez dû saisir l’opportunité de choisir la porte numéro 3 !
Et ce qui est encore plus paradoxal est que si votre choix initial avait été la porte numéro 3, vous auriez dû changer pour la numéro 1 lorsque Monty Hall vous en a donné l’opportunité !
Vous ne me croyez pas ? Voici le raisonnement.
Lors de votre choix initial, chaque porte a une probabilité de 33% de dissimuler la voiture, vous êtes donc indifférent entre les trois portes.
Cependant, lorsque Monty Hall vous révèle que la voiture n’est pas derrière la porte numéro 2, vous disposez d’une nouvelle information qui doit être prise en compte dans les probabilités.
Suite à votre choix initial, vous serez d’accord avec moi que la voiture a 33% de chance d’être derrière la porte numéro 1 que vous avez choisie et 67% de chances d’être derrière l’une des deux autres portes. Cependant, une fois que la porte numéro 2 est éliminée, cela signifie que la voiture a 67% de chance d’être derrière la porte numéro 3 ! Vous devriez donc choisir cette porte puisqu’elle a deux fois plus de chances de cacher la voiture !
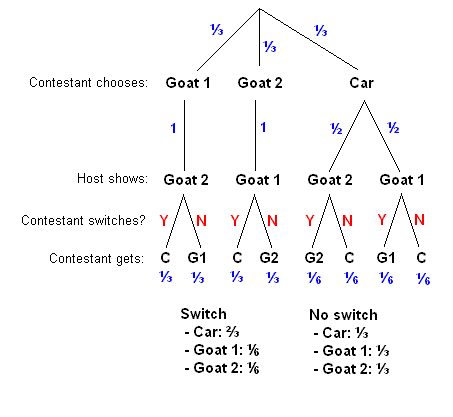
Beaucoup de gens choisissent pourtant de ne pas modifier leur choix, souvent à cause de l’aversion à la dépossession et au biais de statu quo, mais aussi simplement parce que les gens sont aveugles face aux probabilités.
Vous ne me croyez pas ? Vous pensez que ce ne sont que des conjectures mathématiques qui n’ont aucun lien avec le monde réel ?
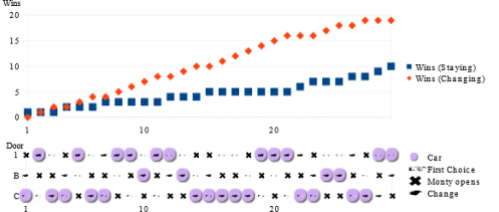
Et bien faîtes le test vous-mêmes avec un jeu de carte ou encore mieux, avec une simulation Monte Carlo. Vous verrez que la stratégie consistant à changer son choix gagne deux fois plus souvent que celle consistant à conserver son choix initial!
Autres exemples
Supposons que la foudre a un risque sur 30 de frapper dans votre ville une journée donnée et que cette probabilité ne change pas d’une journée à l’autre, peu importe ce qu’il arrive.
- Disons que la foudre a frappé votre ville le 1er avril.
- Vous vous demandez quand la foudre frappera la prochaine fois.
- Est-il plus probable que la foudre frappe à nouveau le 2 avril, le 4 avril, le 10 avril ou le 1er mai ?
La réponse est évidemment le 2 avril, dont la probabilité est 1/30 ou 3,33%.
Pour que la prochaine foudre frappe le 4 avril, il faudrait d’abord qu’elle ne frappe pas le 2, ni le 3.
La probabilité que la foudre ne frappe pas le 2 avril est de 29/30, même chose pour le 3 avril.
Donc :
29/30 x 29/30 x 1/30 = 3,11%
Beaucoup de gens répondent le 1er mai, alors que la probabilité n’est plus que de 1,20%. Ce phénomène peut être décrit pas une loi de Poisson, que le cerveau humain a beaucoup de mal à traiter.
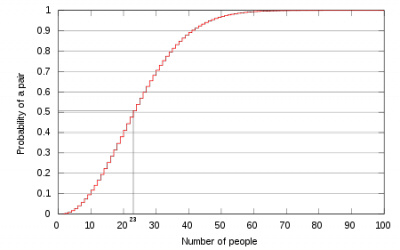
La plupart des gens ont de la difficulté à croire que si 57 personnes se trouvent dans la même pièce, la probabilité que deux d’entre elles aient la même date de naissance est de 99% !
Beaucoup de gens croient dur comme fer qu’au Loto 6/49, la séquence 1-2-3-4-5-6 est moins probable que disons 3-12-21-28-35-47. Pourtant, beaucoup de personnes achètent un billet avec 1-2-3-4-5-6 en se disant, avec raison, qu’un jour, cette combinaison sortira… mais le gain sera faible puisqu’il sera divisé par un nombre record de gagnants.
En revanche, beaucoup pensent que si le chiffre 49 n’est pas sorti depuis 10 tirages, ses chances de sortir au prochain tirage sont plus élevées. C’est évidemment faux, exemple flagrant de l’erreur du parieur.
Supposons que l’on joue à pile ou face, selon vous laquelle de ces deux séquences est réelle et laquelle est fictive (P=pile, F=face) :
1) PPFFPFPPPP ou 2) FPFPPFPFFP
La séquence numéro 1 est typique d’un événement aléatoire (même si elle comprend 4 piles consécutifs), alors que la séquence numéro 2 est fictive. Il est normal d’avoir des séquences de 4 piles, et cela ne signifie pas que le lancer suivant a plus de chance de tomber sur face. En revanche, les séquences parfaitement équilibrées comme la séquence numéro 2 sont plutôt rares.
Conclusion
Sans vouloir me vanter, je ne me fais pratiquement jamais berner par ces paradoxes et biais cognitifs. Cela fait partie de mon travail et j’ai été formé pour cela, ce qui n’est pas le cas de la majorité de la population. Cependant, je dois avouer qu’il m’a fallu réfléchir plusieurs minutes avant de bien saisir le problème Monty Hall. Néanmoins, même les gens éduqués, inclus des mathématiciens, se font initialement duper par ce problème ; ce n’est pas tant une question d’intelligence. Seulement 13% des gens décident de changer leur choix de porte !
Je trouve ces petits paradoxes mathématiques fascinants, car ils nous montrent à quel point le cerveau humain est vulnérable étant donné sa propension à prendre des raccourcis qui mènent souvent à un ravin.
L’être humain est définitivement irrationnel, tel que démontré hors de tout doute par, entre autres, Daniel Kahneman et Amos Tversky, et cela est en partie attribuable à son incapacité à bien évaluer les probabilités.
Dans ce contexte, il est peu surprenant que la population soit si sympathique aux idées politiques populistes telles que le salaire minimum à $15, le protectionnisme ou encore les subventions…
Pour en savoir plus :
Wikipedia : Problème de Monty Hall
—



Merci pour cet article aussi surprenant qu’intéressant.
comme quoi .. le cerveau n’a pas un fonctionnement mathématique , ce n’est pas une machine.. et que l’IA n’est pas pour demain avec des machines binaire
Oui; nous baignons dans l’irrationnel.
Bien plus que vous ne l’imaginez sur Ce forum.
Votre problème, c’est que vous ne le savez pas…
Vous seriez aimable de nous l’expliquer à l’instar de l’auteur de l’article ci-dessus…
Marxan balance ses petites piques et ne répond ni n’argumente jamais.
Il a une aversion au savoir.
Et comble de l’irrationnel, vous prônez le marxisme…
Peut être que le cerveau est habitué à traiter des problèmes dans un monde beaucoup plus complexe que ces situations simplistes, et surtout face a des agents qui ont des intentions souvent cachées et ambiguës. Le cas des trois portes s’explique mieux du coup: “s’il veut me faire changer de choix c’est qu’il a plus à y gagner”. Ce raisonnement fonctionne dans la vie RÉELLE, et c’est cela qui est important.
Je suis d’accord de penser que notre cerveau a évolué de cette façon pour nous faire prendre des décisions rapides face à des situations de danger ou d’urgence. Préhistoriquement, nous n’avions peut-être pas toujours le luxe de la réflexion et nous devions penser “binairement”, agir ou ne pas agir, bouger ou rester immobile. Le risque de l’aversion est très ancré dans notre psyché. Dans le cas de l’expérience des portes, on remesure à nouveau le risque.
Le cerveau n’a simplement pas un fonctionnement optimal. Comme toute chose que l’on construit petit à petit en partant de l’essentiel et en le perfectionnant. La prise en compte finale de tous les paramètres imposerait une autre structure, mais la structure initiale a été conçue avec seulement une partie des paramètres :
“Vingt fois sur le métier remettez votre ouvrage, Polissez-le sans cesse, et le repolissez, Ajoutez quelquefois, et souvent effacez.” Boileau, L’Art poétique.
Quand on conçoit, invente, développe … on s’aperçoit que l’on a intérêt à repartir à zéro. Avec notre cerveau, il faudrait attendre des millénaires de mutations génétiques pour faire émerger une toute nouvelle espèce. Il faut bien faire avec ce qu’on a …
je ne sais pas si notre cerveau nous trompe mais à l’évidence le moindre calcul de probabilité demande un peu de calcul et pour la majeure partie des gens, de prendre une feuille un crayon…. il n’y a pas que les probabilités..il en va de m^me pour des petits problème requérant la solution d’une équation à deux inconnues , j’en ai fait l’expérience ..reste que le paradoxe de monty hall. fait partie de ces trucs qui nous énervent et sont extrêmement salutaires.. rien que pour ça merci.
J’ai un peu de mal avec la formulation..pourquoi serait ce notre cerveau qui nous trompe puisque c’est notre cerveau qui nous apporte la solution si on s’en donne la peine…??? On pourrait dire que c’est notre instinct qui est mauvais, mais l’instinct doit aller vite…
et si je vous demande de me répondre _vite_ pour savoir quelle est la probabilité que 2 ( 2 au moins!) d’un groupe de 12 personnes aient la même date anniversaire…l’instinct ne sert pas à grand chose..
En outre, les probabilités ont cette particularité…ça ne nous sert pas à grand chose, car elle sont utiles pour les grands nombres et pour un seul événement ça n’aide pas…on peut juste dire ‘ai eu du bol ou pas…, regardez le monty hall, dans le monde réel les gens savent que deux chances sur trois ou 1 chance sur trois….c’est toujours ne pas être sûr de gagner…qualitativement pareil. et si dans ce paradoxe vous ne changez pas de porte vous avez encore une chance significative de gagner … et ça l’instinct le sait…
je vais ajouter ceci,..un statisticien fait souvent des hypothèses certaines impossibles à vérifier… en général il POSE que ceci ou cela est aléatoire, il DÉDUIT une probabilité…
mettons que une personne tire au dés..12 fois et que 10 fois le 6 sorte… que pouvez vous en conclure sur ce dé ? qu’il est pipé ou que vous avez observé un tirage comme un autre? les probabilités ne permettent quasiment jamais de conclure..
Où est l’aléa?????????
Le statisticien déduit à la fois une probabilité et un intervalle de confiance. Il y a une discussion intéressante de ce point chez Taleb, dans Le Cygne noir je crois. L’intervalle de confiance, pour des événements rares, perd son importance. La probabilité de tirer 10 fois le 6 sur 12 tirages est suffisamment faible pour que l’on puisse la négliger devant celle d’une arnaque, conclut Taleb…
Ceci étant, le raisonnement comme quoi les statistiques et les probabilités ne devraient pas s’appliquer à un choix lorsqu’on fait un seul et unique tirage “aléatoire” est parfaitement défendable, mais il vaut mieux le décider alors en pleine connaissance de cause et éviter d’appeler les probabilités à la rescousse pour justifier son choix.
“La probabilité de tirer 10 fois le 6 sur 12 tirages est suffisamment faible pour que l’on puisse la négliger devant celle d’une arnaque…”
Taleb néglige le problème de la longue traîne même s’il en parle un peu.
Observez la probabilité d’avoir 10 fois le 6 ou 10 fois le 5 ou 10 fois le 4 ou 10 pairs ou 10 impairs ou 10 suites… etc… et ce nombre cumulé d’événements “rares” devient tout à coup aussi important que le nombre d’événements dont la somme des probabilités est de 0.5 et donc un de ses événements “rare” se produira forcément même si sa probabilité est de 0.00001.
De nombreux business plans sont bâtis sur ce principe et en tout premier Amazon avec ses livres (mais aussi d’autres produits). Amazon vend plus de livres parmi les faibles tirages, voire à l’unité que de best sellers.
Ce phénomène est connu depuis très longtemps, Taleb l’a juste popularisé mais il ne l’a pas découvert.
Tout à fait, Taleb est surtout quelqu’un qui sait comprendre, expliquer et remettre dans le contexte quotidien les théories statistiques de haut niveau. Lui-même si j’ai bien compris, a su tirer profit des sous-estimations communes des probabilités d’événements rares. Néanmoins, je le suis et le soutiens, d’expérience, sur le fait que la plupart du temps des facteurs nouveaux et négligés auparavant sont plus probables que les événements rares “théoriques”. Si vous analysez du “big data”, quelques centaines de millions de valeurs, vous pouvez aller à 5, 6 écarts-type, néanmoins vous verrez que dans les 90% des extrêmes sont des erreurs de mesure.
Je m’interroge cependant sur l’histoire de la foudre.
Si chaque jour on a 1/30 de chance, pourquoi n’y a-t-il pas autant de chances que la foudre frappe n’importe lequel des jours que vous citez ?
J’aurais dit que le fait qu’il y ait eu foudre les veilles n’influe pas sur la probabilité d’avoir la foudre le jour donné donc 1/30 à chaque nouveau jour.
Oui, c’est est le sens d equiprobable, toujours la même erreur sur les probabilités conditionnelles.
D’accord avec Pam. j n’arrive pas à être convaincu. La probabilité est la même pour chaque jour. Elle peut retomber le lendemain comme dans trente jours. L’auteur lui-même affirme qu’il n’y a pas d’incidence. C’est comme le coup avec les trois portes. La probabilité ne change pas qu’elle tombe un premier mai même si on constate qu’elle n’ait pas tombé les jours précédents.
L’auteur méconnait les probabilités conditionnelles.
Si, a priori, la voiture a 1/3 chance de se trouver derrière l’une quelconque des 3 portes, SI on sait en plus qu’elle n’est pas derrière la porte N°2 (information supplémentaire) les probabilités se modifient.
La voiture a désormais 1/2 chance de se trouver derrière l’une des 2 portes au contenu caché.
Le bon sens ne s’oppose pas toujours aux probabilités, encore faut-il ne pas trop les maltraiter.
Pour la loterie le raisonnement est juste, question d’espérance de gain.
Pour perdre le moins possible statistiquement (le seul gagnant assuré est l’État), chaque tirage étant équiprobable, il faut parier sur les combinaisons les moins jouées.
En effet.
Uniquement quand l’énoncé n’est pas clair.
C’est du niveau 1ère, je mets un lein Wiki
https://fr.wikipedia.org/wiki/Probabilit%C3%A9_conditionnelle. Extrait :
“La notion de probabilité conditionnelle permet de tenir compte dans une prévision d’une information complémentaire. Par exemple, si je tire au hasard une carte d’un jeu, j’estime naturellement à une chance sur quatre la probabilité d’obtenir un cœur ; mais si j’aperçois un reflet rouge sur la table, je corrige mon estimation à une chance sur deux. Cette seconde estimation correspond à la probabilité d’obtenir un cœur sachant que la carte est rouge. Elle est conditionnée par la couleur de la carte ; donc, conditionnelle.”
Le “Sans vouloir me vanter, je ne me fais pratiquement jamais berner par ces paradoxes et biais cognitifs. Cela fait partie de mon travail et j’ai été formé pour cela, ce qui n’est pas le cas de la majorité de la population.” est assez comique, l’auteur aurait dû se méfier de la foudre qui tombe un .. 1er avril !
Je le répète les probabilités conditionnelles c’est du niveau 1ère scientifique, un pro de l’investissement devrait connaitre.
pam : Le mot que vous avez omis est «à nouveau», pour la première fois. Il est évident qu’en prenant cette définition la probabilité pour que la foudre frappe la ville dans 5 ans pour la première fois est nulle, pas la probabilité pour qu’il y ait la foudre ce jour-là (qui reste d’1/30). Il n’y a rien de contradictoire.
Christial : vous vous trompez, l’auteur a parfaitement raison. Pour vous en convaincre, prenez 100 chèvres au lieu de 2. La probabilité pour que la joueur ait choisi correctement la bonne porte du premier coup est très faible. Si les 99 chèvres sortent le joueur a tout intérêt à changer de porte. Le fait d’indiquer où se trouvent les chèvres a posteriori ne peut pas influer sur la probabilité de trouver une voiture en gardant la première porte sachant que le choix a été fait sans cette information. Par contre la probabilité augmente de façon considérable pour la deuxième porte restante, qui doit être de 1-1/30 = 29/30. C’est exactement ce qui se passe pour 2 chèvres mais c’est moins apparent.
Je voulais écrire 99/100 et 1/100.
Étudiant, je suis au regret de vous mettre un 1/20.
La probabilité initiale de tomber sur la voiture est de 1/3 ; la probabilité conditionnelle pour un nouveau choix, sachant que la porte N°2 n’est pas la bonne, devient 50%.
Et si la porte cachant la 2ème chèvre était aussi dévoilée, alors la nouvelle probabilité conditionnelle passerait à … 100 %. Là au moins vous serez d’accord avec moi, sinon je vous mets 0/20 !
Les probabilités évoluent avec l’information, phénomène bien connu des initiés et des … professionnels de l’investissement, d’où l’intérêt en Bourse des logiciels.
@Christal :
Pour les gens qui comprennent lentement comme vous, il y a une vidéo de 20 mn en fin d’article qui explique tranquillement le paradoxe de Monty Hall. Vous devriez la visionner avant de distribuer vos bons points.
L’analyse peut se faire de façon rapide : il y a 2 chances sur trois d’avoir désigné une porte derrière laquelle il y a une chèvre, une fois la seconde porte désignée, il reste une chèvre et une voiture, il y a donc 1 chance sur deux d’avoir une voiture derrière la dernière porte…
quelques ligne de PHP pour faire la demonstration :
[code]
$choices=array(1,2,2);
$good=1;
$max=100000;
for($i=0;$i $c){
if($c != $choosen && $c != $good && count($cards) > 2 ){
unset($cards[$k]);
}
}
if($choosen == $good){$keep++;}
else{$change++;}
}
echo ” Keep : $keep / Change : $change”;
[/code]
Pour les sceptiques, cette simulation (de 100000 fois) donne precisement le meme resultat que l’auteur, et marche quelle que soit le nombre de portes (“cards)”.
quelques ligne de PHP pour faire la demonstration :
https://gist.github.com/anonymous/fd32df949e8bbe9c0c2c7395e8c915e9
Pour les sceptiques, cette simulation (de 100000 fois) donne precisement le meme resultat que l’auteur, et marche quelle que soit le nombre de portes (« cards) ».
PS : pour la modération, Mon commentaire précedent est tronqué, et ne peux donc pas fonctionner. Merci de le supprimer, et de garder celui ci , à la place qui pointent sur le code complet ,-)
Non justement. Il n’y a pas de réévaluation des probabilités une fois que l’on ouvre un porte: si tel était le cas, cela voudrait dire que l’on réévalue l’emplacement de la voiture, qui serait alors d’une chance sur deux.
Hors justement, la voiture ne bouge pas, et la probabilité reste de 1/3 par porte unitaire.
vu que les deux autres portes représente donc 66% du choix de la bonne réponse, et que l’on a ensuite une mauvais porte qui est éliminée du choix, cela conserve 1/3 de chance pour la porte choisie initialement, et 2/3 pour la porte restante.
@pam: Relisez l’énoncé : “…quand la foudre frappera la prochaine fois.”
Pour une date autre que le 2avril, il faut que la foudre ne soit pas tombé un jour précédent !
Exact! La plupart des gens ignorent de considerer “la prochaine fois”.
Dans des expériences menées en anglais, on mettait le mot “next” en gras, mais les gens n’en tenait pas compte.
Effectivement, j’avais zappé l’information.
Merci pour l’article !
Pam, comme vos petits camarades vous faites une mauvaise lecture de l’énoncé. On parle de la PROCHAINE foudre après celle étant tombée le 1er avril.
On ne parle pas de la 4ème, de la 5ème ou de la 12ème… mais de la 2ème.
oops, sorry, je n’avais lu que la 1ère salve de réponses à Pam…, celle des gros malins qui n’ont déjà pas compris l’énoncé 😀
Sérieux besoin de travailler les probabilités conditionnelles !
Désolé, mais j’adhère pas. En tout cas, pour le premier problème (les 3 portes). Il me semble que lorsque les données changent (un choix de 2 portes au lieu de 3 initialement) le jeu des probabilités change aussi.
L’auteur peut frimer en prétendant qu’il est formidable et ne se fait jamais berner, mais je me permets de prétendre que lorsque les données à analyser changent, celui qui continue de fonder son raisonnement, fût-il mathematique et statistique, sur les anciens paramètres se gourre copieusement……
Ah Ces mathématiciens, pour eux le rationnel est forcement que mathématique…
Sur le premier problème, statistiquement ça ne change pas. Il faut décoder le petit dessin en arborescence, mais l’auteur n’a pas tort. Il faut comprendre que le cerveau humain ne se résume pas à une calculatrice et que nous avons aussi des conditionnements psychologiques qui remontent à la préhistoire qui nous font prendre de décisions “non-mathématiques”.
Avec le problème des trois portes, il n’ y a pas de nouveau tirage. La voiture n’a pas bougé. Il y a toujours une chance sur trois qu’elle soit derrière. Qu’on nous montre une chèvre induis un biais dans notre raisonnement global (qui n’est pas que basé sur les probabilités).
Par contre je ne le suis pas sur le problème de la foudre qui tout au contraire va à contre courant de ce qu’il explique avec le problème des trois portes. Surtout il contredit l’énoncé du problème. Il jongle avec les chiffres et tente vainement de nous expliquer qu’un évènement à plus de chance d’arriver dans un futur proche que lointain. Inversement, je pourrais penser qu’au fur et à mesure des jours, la foudre a d’avantage de chance de tomber un premier mai ! Alors que la probabilité ne change pas.
@Christial, GL et tous les autres qui n’ont pas compris
Cette expérience a été testée dans le monde réel et les résultats confirment que la stratégie de changement de choix gagne deux fois plus souvent (67% contre 33%).
Je l’ai même fait moi-même, avec des cartes en guise de portes. j’ai joué 100 fois et tout concorde.
Je trouve incroyable que meme si on vous l’explique, vous persistiez malgre tout dans l’irrationnel…
“les autres qui n’ont pas compris”
Votre démonstration ne démontre rien à part qu’une chance sur 3 est inférieure à 1 sur 2, soit une évidence !
C’est vous qui montez un sophisme et faite un lien entre 2 propositions indépendantes !
Proposition 1 ne peut pas être comparé à Proposition 2. Quand le candidat préfère garder la porte 1, il est dans le cas de la proposition 2, pas la 1. Le fait qu’il s’agit des mêmes portes vous permet de faire une confusion alors que la proposition 1 est forcément annulée !
Vous êtes dans l’irrationnel, la confusion entre 2 choses non comparables !
@Amike, GL et Christial:
On applique le théorème de Bayes (on enchaîne en fait deux probabilités conditionnelles) et on obtient bien 2/3 versus 1/3.
Je vais le faire de façon intuitive:
Imaginez 1 millions de portes, avec le gros lot derrière une seule des portes. Vous désignez une porte. Vous conviendrez que la chance que le gros lot soit derrière votre porte est quasi nulle (1 sur 1 million). Il a toutes les chances d’être derrière une des 999.999 autres portes.
Sachant que le gros lot est vraisemblablement (en fait 999.999 chances sur 1 million) derrière l’une de ces portes plutôt que la votre, supposez maintenant que l’on désigne l’une après l’autre parmi les autres portes celles ne contenant pas le gros lot jusqu’à ce qu’il n’en reste qu’une. Au final il reste votre porte qui n’avait (pratiquement) aucune chance de contenir le gros lot et une porte de l’ensemble de celles qui avaient toutes les chances de contenir le gros lot.
D’après vous, le gros lot est derrière quelle porte la votre, ou l’autre qui reste?
Si vous répondez “votre porte”, ce n’est pas que vous ne comprenez pas, c’est que vous êtes complètement crétins. Et à cela il n’y a plus rien à faire.
En fait, meme des gagnants de prix nobel de physique sont tombe dans le piege!
Je ne prétends pas le contraire, dans la version à trois portes il est très difficile de sentir la réponse; la plupart des gens (vous et moi compris) peut facilement se tromper, ce même si on a fait beaucoup de mathématiques, de logique et de probabilité ou qu’on a vu de nombreuses tâches de ce genre. Je suis économiste et psychologue, senior lecturer à l’université, donc des maths j’en ai fait et des tâches de ce genre j’en ai vu des charrettes, et pourtant, il m’arrive encore de trouver des tâches de raisonnement construites par des psychologues dans lesquelles je me mets dedans. A chaque fois je suis émerveillé de voir comment mon intuition me guide mal.
Par contre, quand on expose la version aux 1 millions de portes, pas besoin de faire de calcul, l’intuition que cela génère chez pratiquement tout le monde conduit à la bonne réponse: il faut changer de porte. Là, comme je le dis ironiquement, celui qui ne comprend pas, ce n’est pas qu’il ne comprend pas……..
Ceci étant dit, j’en profite pour vous remercier pour votre blog “le minarchiste”. Je vous lis régulièrement, c’est un des deux ou trois meilleurs blogs/podcast/site/etc du net pour moi. Un vrai régal. j’y découvre souvent une lecture ou un auteur que je ne connais pas.
Continuez.
@Libertarien
Merci!
@ Minarchiste
“Je trouve incroyable que meme si on vous l’explique, vous persistiez malgre tout dans l’irrationnel…”
Bah, comme les socialistes en fait… on n’est pas sorti de l’auberge !
Si on créait un état libéral, ils arriveraient encore à dire que c’est un coup de bol si ça marche !
Pour ce qui est des portes le problème devient plus facile à comprendre si l’on prend 100 portes et que l’on en dévoile 98. Là la personne ne peut pas dire que les 2 restantes sont à 50/50. Celle choisie est à 1/100 et celle non choisie à 99/100.
Parfaitement d’accord avec vous. Après l’ouverture d’une porte ´les probabiltes sont redistribuées à 50/50 entre les 2 portes restantes.
Mea culpa. Il faut du temps pour comprendre mais l’auteur a raison. Voir Wikipedia .
Ben oui LpV ! Tout à fait d’accord.
L’Humain est aveugle aux probabilités…
Sans doute parce qu’il est avant tout un être de relations humaines qui ne relèvent pas de conjonctures mathématiques.
Lequel d’entre nous a eu à choisir d’ouvrir une porte sur trois et de découvrir derrière une chèvre ou une voiture ?
Par contre, nous avons tous eu à tenter d’anticiper ou décrypter le comportement de tel ou tel de nos congénères.
Faisant partie des 13% de la population ignorante en matière de probabilités, j’avoue ne pas comprendre pourquoi dans l’exemple des 3 portes, seule la porte non choisie voit son taux de probabilité augmenter à 67%
Le choix réduit à deux possibilités plutôt que trois devrait modifier le taux des deux portes restantes et pas une seule non…?
L’aspect essentiel dans ce problème est que le présentateur n’ouvre pas une porte au hasard mais ouvre forcément une porte qui contient une chèvre.
Si il ouvrait une porte au hasard et u’une chèvre s’y trouvait, alors on aurait bien 50/50 entre les deux portes restantes.
Par contre, ce n’est pas le cas ici :
-On a choisi une porte sur 3 avec donc 1 chance sur trois de gagner.
-Il y’a 2 chances sur trois que la voiture se trouve dans l’une des deux autres portes. Si on pouvait choisir les deux portes à la fois, on aurait 2 chances sur 3 de gagner.
-il y’a au moins une chèvre dans les deux portes qu’on n’a pas choisi et comme le présentateur connait le contenu des portes, il élimine une des mauvaises solutions.
– la probabilité de deux chances sur trois se trouve donc maintenant sur une unique porte.
La science au service de l’idéologie: rien de neuf sous le soleil. Au delà des ratiocinations ideoprobabilistes, la question essentielle est celle-ci: quel est le domaine de rationalité du rationnel ? Rappelons ici qu’en mathématique les axiomes d’une part, en physique les constantes universels sont des objets dont la propriété irréductible est d’être irrationnels. La question se réduit dès lors à celle-ci: l’homme peut-il dominer l’univers grâce à son intelligence, peut-il s’affranchir des biais de sa constitution ? Dit plus abruptement: est-i possible de renouveler l’homme? Le XXème siècle a tenté l’aventure à plusieurs reprises. Dit encore autrement, la cognition, ou l’esprit si l’on préfère, est-elle une chose du monde, ou lui est-elle extérieure ? Le choix de l’auteur est le second. De sorte que l’apparente irrationalité du monde, dont l’homme est partie, reflète simplement l’impossibilité de l’esprit humain à rendre compte de dimensions si profondes qu’elles sont inaccessibles au discours rationnel, bien qu’en réalité elles le sous-tendent, comme les axiomes, postulats irrationnels et nécessaires, sont les fondements de la géométrisation du monde, rationnelle dès lors qu’est dépassé le seuil de l’axiome. En deçà, rien n’est connaissable. Ce qui signifie que la rationalité intrinsèque de cet en deçà ne nous est pas accessible, car elle conditionne la possibilité même de connaître. Au delà de ce seuil, tout est potentiellement connaissable, bien que construit sur le sable de l’inconnaissable.
L’exercice concernant la foudre est faux. L’auteur – les mathématiciens ont rarement la maîtrise fine des rationalités dérivées du langage – oublie de préciser que les probabilités de deux foudroiements consécutifs ne sont pas indépendantes. On ne va nulle part avec un énoncé vicié. Outre cette lourde erreur formelle, la physique au surplus contredit l’affirmation de la dépendance des foudroiements. Mais avec des “si”, il n’est pas si difficile de mettre Paris en bouteille.
On se calme. Ce n’est pas une énigme de physique. Je sais bien que si la foudre frappe aujourd’hui, il est moins probable qu’elle frappe demain, même chose pour les tremblements de terre.
C’est un problème de probabilite. L’exemple utilise n’a pas d’importance.
Parfaitement d’accord, la foudre ne doit pas être utilisée comme exemple car elle dépend de lois diverses, pas du seul hasard…
un choix humain n’a rien de hasardeux , il est déclenché par la variable que l’on connait le mieux d’un problème posé , dans le cas des portes la variable choisie sera .. le présentateur .par contre , si il n’y a pas d’intervenant humain ,donc de variables connues, le choix sera basé sur … un humain virtuel.
les probabilités de choix d’un humain sont impossibles a calculer sans données historiques…donc, le cerveau est capable de faire un calcul de probabilité basé sur son expérience vécue de situations similaires..mais ce calcul ne sera pas dans les normes mathématiques , le cerveau ne sait pas ce qu’est 1+1 si on ne lui dit pas et il s’en fout , ce qu’il veut , du plaisir rien que du plaisir et ce plaisir vient lorsque ces choix sont de bons choix et donc ne lui impose pas d’autres problèmes a résoudre .
intéressant, le cerveau a effectivement un problème de discernement mais ce problème n’est pas inhérent aux statistiques/probas, malgré vos références diverses dans l’article, j’ ai déjà eu l’occasion de voir des problèmes similaires dans d’autres matières. En réalité le cerveau utilise souvent un raccourci pour diverses raisons (la principale étant probablement le gain de temps) et se trompe donc sur des problèmes qui semblent à posteriori logiques.
de tête je n’ai que quelques exemple : celui qui par exemple a perdu de l’argent, aura indépendamment des probabilités la volonté de miser plus que celui qui n’en a pas perdu. ( ici c’est encore un autre problème)
Il y a aussi une multitude d’exemples sur les raccourcis effectués par le cerveau concernant les formes et couleurs, ou encore tout simplement par la magie (tours de passe-passe).
Le cerveau essaie de retrouver un schéma familial et rationnel dans le processus qu’il vient de voir et se fait donc berner.
En effet sans cette capacité à tout simplifier il faudra un temps énorme pour analyser toutes les situations, est ce que le truc rond et rouge dans mon assiette est une tomate? est ce que l’objet que j’ai depuis 3 ans autour du bras est une montre etc
Outre le fait que les probabilités conditionnelles ne soient pas prises en compte, l’auteur ne réfléchit pas non plus sur la voix, l’intonation. Or la façon avec laquelle la phrase est dite peut apporter des renseignements ou induire en erreur le joueur sauf bien sur si Monty avait en permanence une voix monocorde ce dont je doute.
Oui, plus généralement, si l’énoncé est différemment exprimé, le choix des candidats change. Donc, l’affirmation d’une incapacité humaine sur les statistiques est fausse puisqu’elle dépend fortement de la manière dont est exprimé ou rédigé l’énoncé ou la capacité du candidat à en comprendre les subtilités.
Le paradoxe de Monthy Hall est un faux paradoxe statistique.
L’astuce repose sur les termes de l’énoncé.
Si le paradoxe de MH devait servir à montrer la faiblesse humaine des statistiques, il aurait fallu changer l’énoncé ainsi :
“Vous avez fait un choix parmi 3. Si je retire une mauvaise porte, voulez vous refaire un choix parmi 2 ?”
Ainsi exprimé, j’ai beaucoup de doute que seul 13% des candidats préfèrent 1 chance sur 2 plutôt que 1 chance sur 3.
Quant à la démonstration du meilleur choix (le graphe), elle est tout simplement impossible : En choisissant ou non la porte 3, j’annule mon premier choix ! De même en gardant le premier choix, j’élimine la suite ! En gros, l’expérience du chat de Schrödinger pris au premier degré !
Au final, le mauvais choix des candidats (en moyenne) est surtout dû aux biais psychologiques habituels.
PS: Bien sûr, avec l’école moderne, le 100% sur l’évaluation de l’expression 50%>33….% serait inespéré…
PS2: Je ne lirai plus les articles du Minarchiste sans un léger doute…
pour les portes d accord avec le minarchiste et l etudiant
au depart 2 chances sur 3 de choisir une chevre donc faux 2 / 3 et bon 1/ 3
si faux le presentateur est oblige de choisir la derniere chevre puiqu il reste une chevre et la voiture
donc la voiture est derriere la derniere porte et j ai interet a changer mon choix
et j ai 2 fois plus de chances d avoir faux au depart
si bon au depart alors ok au 2eme tour 1 chance sur 2
Le paradoxe de Monthy Hall, ou comment des statisticiens se prennent les pieds dans l’intitulé d’énoncés retors…
J’ai relu à nouveau l’énoncé original :
“Il vous demande d’abord de choisir l’une des trois portes (supposons que vous choisissiez la porte numéro 1).
Puis, Monty Hall ouvre l’une des deux autres portes derrière laquelle il sait qu’il y a une chèvre (disons la porte numéro 2).
Finalement, il vous demande si vous désirez modifier votre choix.”
Et l’auteur de conclure qu’il faut modifier son choix, car il a une meilleure espérance.
—————————————–
Or voici mon analyse:
– 2 questions sont posées successivement au candidat.
– Si le choix du candidat est identique aux 2 questions, son choix est évalué sur les conditions de la première (1chanche/3)
– Si le choix du candidat est différent, son choix est évalué sur les conditions de la seconde (1chance/2).
Pourquoi cette différence d’évaluation, puisque finalement j’hésite entre la porte 1 et la 3. Modifier mon choix c’est choisir entre 1 ou 3, et non 1 ou 2 ou 3 !
La tromperie de la démarche repose en la confusion du même résultat (porte 1), qui permet à l’auteur – tel à un jeu de bonneteau – d’inverser les conditions pour arriver au résultat désiré.
Cet article est choquant : il démontre comment au travers d’une démonstration à priori rationnelle, on peut faire passer un message sur la démocratie, tel que le peuple, la majorité, ne serait pas suffisamment compétent ou facilement manipulable !
Pourtant, on voit bien qu’il s’agit d’abord d’un problème d’énoncé confus à dessein, et non d’acquis ! Le problème ici est plutôt celui de la pensée unique, ou en l’occurrence d’un énoncé de jeu imposé, et qu’on n’ose remettre en cause (biais d’autorité).
“Democraty is so overrated”… surtout si le résultat nous déplait !
Oups, mea culpa. L’énoncé est parfaitement correct et précis. Je retire donc ma conclusion.
Le paradoxe de Monty Hall c’est du pipi de minet à côté des découvertes de Benjamin Libet à peu près à la même époque.
Il faut lire “Mind Time” et comprendre que notre libre arbitre se résume au droit de veto car toutes nos décisions sont prises par le corps avant le feu vert du cerveau et donc de la conscience.
La première démonstration est franchement risible car le cerveau se met immédiatement en route pour essayer de comprendre les raisons qui ont fait qu’on ouvre soudain la deuxième porte. C’est le début d’une spéculation sans fin. Et donner 67 % à la porte trois c’est vraiment faire prendre des vessies pour des lanternes car dès le moment où la porte deux a été ouverte, la donne du problème change et la division est révisée en deux portes soit 50/50.
Choisissez une porte parmi 100. Je vous en ouvre 98 autres. Il en reste donc toujours 2 de fermées, la votre et celle que je n’ai pas ouverte.
Vous pensez toujours que la porte que vous avez choisie est à 50/50 ?
@sam player: La porte que le candidat a choisie devient une des 2 qui restent fermée. Donc, oui, la porte choisie a vu sa probabilité monter d’autant que vous supprimiez les autres.
La probabilité au premier choix n’existe plus. Et changer le choix ne rime à rien.
Confirmation : Si vous supprimiez immédiatement les mauvaises 98 portes, les 2 portes restantes sont à 50/50. Ce qui est exactement l’état de la proposition au moment de la deuxième question.
L’information sur le premier choix est un “bruit”, une information inutile !
“Si vous supprimiez immédiatement les mauvaises 98 portes, les 2 portes restantes sont à 50/50. Ce qui est exactement l’état de la proposition au moment de la deuxième question.” cela est vrai si vous oubliez quelle porte vous avez choisis au début et que l’on vous redemande de choisir au hasard.
@zben: Exact, sam player à raison. Si je “garde mon choix”, il est probablement moins bon que l’alternative…
Je suis d’accord avec ce raisonnement. Sachant que quoi que le candidat choisisse, une chèvre sera éliminée, celui-ci n’a en réalité à choisir qu’entre une chèvre et la voiture. En fait le jeu ne commence réellement qu’après l’ouverture de la 1ère porte par le présentateur. Avant ça, ce n’était que du show.
Le candidat a donc bien une chance sur deux, la probabilité ne changera pas et il n’a aucun intérêt à changer de choix, à part son “feeling” si il est médium…
Trois portes et une chance sur deux quelle que soit la porte choisie ? On va bientôt gagner un chevreau laid dans votre affaire…
“Le paradoxe de Monty Hall c’est du pipi de minet à côté des découvertes de Benjamin Libet à peu près à la même époque.”
Sauf que depuis le célèbre article de Libet (1983) on a beaucoup progressé sur la question et que l’interprétation du résultat de son étude a fortement été contestée dans la littérature scientifique. Il faut te mettre à jour.
” Et donner 67 % à la porte trois c’est vraiment faire prendre des vessies pour des lanternes car dès le moment où la porte deux a été ouverte, la donne du problème change et la division est révisée en deux portes soit 50/50.”
C’est faux. Il s’agit d’une probabilité conditionnelle, pas de deux évènements indépendants, parce que la porte qui est ouverte ne l’est pas au hasard, c’est une porte dont celui qui l’ouvre sait à l’avance qu’elle ne contient pas le lot gagnant et c’est la raison pour laquelle il l’ouvre. Et cela, fait toute la différence.
Va lire mon commentaire plus haut avec l’exemple à 1 million de portes.
Aucune avancée scientifique n’a permis d’infirmer l’expérience de Libet sur la latence de 200ms. Au contraire, toutes l’ont confirmée et affinée. “Mind Time” a été écrit par B. Libet en 2012 !
Mais je reviens sur cette histoire de portes. Tous semblent s’en tenir aux faits. Mais personne ne questionne ce qui se passe dans la tête de celui qui doit choisir lorsqu’il voit qu’on ouvre une des portes, changeant ainsi radicalement la question de départ.
Respect pour un écrit d’outre tombe !
Oups, oui, Sam Libet est décédé en 2007. Mais l’ouvrage reprend ses derniers travaux et a été publié en 2009. Sorry pour ces imprécisions.
https://www.bookdepository.com/Mind-Time-Benjamin-Libet/9780674040168
Non c’est la version électronique qui date de 2009.
Dans votre lien, cliquez sur *Also available in Paperback 22,84 €* et vous verrez que c’est 2005, donc de son vivant (Harvard University Press, 2005). Le copyright est de 2004 (premières pages)
Décidément les évidences vous échappent… souvent. 😀
Il est en lecture gratuite ici :
http://www.academia.edu/5113416/Benjamin-Libet_-Mind-Time–The-Temporal-Factor-in-Consciousness
Bien vu ! Pour le reste, je vous laisse à vos évidences. Mais faites l’effort de vérifier que les expériences de Libet n’ont jamais été contestées.
Et donc que tout ce qui est dit ici n’est que du brassage d’air.
Décidément vous faites fort.
Googlez benjamin libet criticism
Sinon je ne vois pas trop le rapport avec le sujet ici car plus qu’une réponse instinctive à un problème pour lequel il est normal d’avoir une mauvaise appréciation, il s’agit de compréhension basique de la solution clairement expliquée.
Mais peut-être qu’en fait votre cerveau est bizarrement câblé.
Je doute que nous avancions ici, sam.
Il n’y a pas de compréhension basique, pas plus qu’il n’y a de solution clairement expliquée. Ce sont vos fantasmes et votre besoin irrépressible d’explications qui justifient votre angoisse qui transpire derrière chacune de vos phrases. Surtout dans le ton.
Vous pouvez googler tant que vous voulez, libre à vous de faire confiance au big brother de notre temps, vous ne pourrez vous faire une opinion objective sans aller à la source et sans vérifier par vous même.
Maintenant, si ce qui vous distrait c’est la polémique, alors ok, mais je vous prie de choisir un autre punching ball. Je ne cherche nullement à faire valider mon point de vue. Je me limite à communiquer à qui veut l’entendre les découvertes de Libet et leurs implications qui remettent profondément en cause toute cette discussion.
Vous n’avez pas répondu sur les 100 portes. Vous changez votre choix ou pas ?
Rappel:
Choisissez une porte parmi 100. Je vous en ouvre 98 autres. Il en reste donc toujours 2 de fermées, la votre et celle que je n’ai pas ouverte.
Vous pensez toujours que la porte que vous avez choisie est à 50/50 ?
Quelle insistance Sam !
Vous persistez à ne voir que le calcul des probabilités mathématiques qui vous donnent évidemment raison. Je viens suggérer autre chose, comme nombre de commentateurs ici. Lorsque vous avez décidé d’ouvrir une ou 98 portes, vous avez radicalement changé la donne du problème. Donc je vais aussi changer, ou pas, mon choix.
Cette critique de Libet est intéressante à plus d’un point :
http://www.academia.edu/378015/A_critique_on_the_falsification_of_free_will_by_using_Libet-style_experiments_REVISED_AND_EXPANDED_VERSION_
Les découvertes expérimentales de Benjamin Libet ne viennent que confirmer une intuition philosophique très présente chez les Grecs, les stoïciens en première ligne. Elles viennent déranger, surtout ici, puisqu’elles remettent en cause les fondements du mouvement libertarien avec la notion de responsabilité individuelle.
Je comprends mieux votre position pour défendre cette expérimentation aux résultats sujets à interprétation et à votre absence d’esprit critique. Je le sentais venir le “c’est pas de ma faute”…
Toujours est-il qu’il n’y a pas plus de rapport maintenant qu’avant avec le sujet en cours : les erreurs de perception sont légions dans le monde qui nous entoure.
“Bien vu ! Pour le reste, je vous laisse à vos évidences. Mais faites l’effort de vérifier que les expériences de Libet n’ont jamais été contestées.
Et donc que tout ce qui est dit ici n’est que du brassage d’air.”
Tu veux dire par exemple que les articles comme celui-ci qu’on compte par dizaines dans la littérature scientifique n’existent pas?
Zhu, J. (2003). Reclaiming volition: An alternative interpretation of Libet’s experiment.Journal of Consciousness Studies, 10, 61-77.
Ou comme:
Trevena, J.A., & Millier, J. (2002). Cortical Movement Preparation before and after a Conscious Decision to Move. Consciousness and Cognition, 11, 162-190.
Ou encore celui-là:
Kellera, I. & Heckhausen, H. (1990). Readiness potentials preceding spontaneous motor acts: voluntary vs. involuntary control Electroencephalography and Clinical Neurophysiology, 76, 351-361.
T’en veux d’autres? Parce qu’il y en a des pleines brouettes de travaux qui génèrent des explications alternatives et/ou qui contestent l’explication de Libet…..
Redis-nous qui brasse de l’air?
En fait on comprend de ce que tu dis que d’une part en réalité tu n’as pas idée de ce que montrent vraiment les expériences de Libet, mais qu’en plus tu confonds allègrement “expérience” et “explication”, ce qui montre non seulement que tu ne comprends rien au phénomène dont tu parles, pas plus que tu ne comprends l’épistémologie et la méthode scientifique.
Je crois que c”est toi qu’on laisse à tes évidences coco……..
C’est l’explication qui est contestée coco, pas le résultat de l’expérience ou sa répétabilité.
Quand tu lis ton détracteur, lis-le comme il faut avant de lui faire dire ce qu’il ne dit pas.
Expérience et interprétation ne sont pas des mots interchangeables comme s’il s’agissait du même concept.
Tu devrais faire un peu d’épistémologie des sciences, cela t’évitera de dire des énormités.
Dans ce dernier ouvrage, Libet suggère justement l’intervention de mécanismes inconscients en amont de la décision. Ce qui met sérieusement à mal toutes les théories sur la rationalité et qui, au contraire de la tentative de démonstration du Minarchiste, confirme l’importance de l’intuition qui puise en permanence dans cette vaste source de données. Libet reste factuel et scientifique dans son approche. Maintenant, si l’on transpose ces informations à la psychologie et à la spiritualité, le vertige commence à nous prendre et nous touchons aux notions d’universalité que je ne développerai pas ici, car ce n’est pas le sujet. Avatar, le film, est un bon début de vulgarisation.
Personne ne conteste qu’il y ait une dimension inconsciente ou automatisée dans nombre de comportements. Les travaux de Bargh et bien d’autres sont là pour l’attester. Ce qui est contesté c’est l’explication donnée à l’expérience de Libet. Assurément, on voit que tu ne comprends absolument pas ce que je dis ergo, le contenu dont tu parles.
Je vous sens sur la défensive Libertarien. L’agressivité dans vos propos est révélatrice. Oserais-je vous suggérer de vous détendre et tenter de comprendre que les expériences de Libet sont en fait très prometteuses pour l’humanité.
En effet, depuis le match entre Lee Sedol et AlphaGo, nous avons enfin compris que la machine était considérablement plus efficace que le cerveau. Sauf que… notamment grâce à Libet, nous savons que la machine n’aura jamais cette capacité d’apparence anodine qui consiste à dire non à une information qui s’impose. C’est là que réside vraiment le libre arbitre et cette capacité déjouera toujours la machine en raison de son apparente aberration à laquelle il est impossible de répondre.
Si vous avez suivi les parties, vous aurez compris que le move 78 (4ème partie) de Lee a été permis suite au move 37 d’AlphaGo (3ème partie). Ainsi l’humain a profité d’une incongruité pour procéder de la même manière. C’est véritablement là que la machine va montrer ses limites.
La machine ne pourra jamais prendre la décision de se saborder.
non vous avez faux comme 60¨%des gens ici, il y a bien 67%
Pour le problème des chèvres, posons le légèrement différemment :
Imaginons 100 portes avec derrière 1 voiture et derrière les autres 99 chèvres.
Vous choisissez une porte (la numéro 12 par exemple). Ensuite, j’en élimine 98 avec une chèvre derrière. Il n’en reste donc que 2.
Changer vous ou gardez vous votre choix initial ?
Avez vous plus de chance de gagner en gardant votre choix initial ou en changeant ?
J’entends bien l’histoire des trois portes d’un point de vue mathématique mais pourquoi l’humain suit un autre raisonnement, hérité de notre passé préhistorique ? Une petite histoire pour comprendre pourquoi on ne choisira pas nécessairement une autre porte…
On connaît (presque tous) Jurassic Park. Dans ma petite histoire, Alan Grant le Paléontologue et Ian Malcom le Mathématicien cherche à échapper à deux vélociraptors (plus stressant de tomber sur une de ses bêtes que sur une chèvre). Ils ont trois portes, trois chemins à choisir. L’un d’eux seulement serait sûr.
Ils s’apprêtent à choisir celle qui passe par le lobby quand soudainement un vélociraptor montre sa tête, venant des cuisines. Le paléontologue est prêt à s’engouffrer dans le lobby quand Ian Malcom le mathématicien l’arrête et veut le convaincre de choisir l’autre porte menant vers le garage. “On a pas le temps Ian avec vos devinettes mathématiques, Ian, fuyons ! On tente notre chance !” – “Ecoutez-moi Alan, laissez-moi vous dessinez ce joli diagramme et aaarggghhh !”
Trop tard le vélociraptor avait eu le temps de se jeter sur le mathématicien alors que le paléontologue fonçait à travers le lobby. Il eut de la chance et repensa à cette histoire de probabilité dans l’hélicoptère. “Une chance sur trois, une chance sur deux… Il y a des situations où on a pas le luxe d’une réflexion rationnelle. Heureusement que notre cerveau nous force à prendre des décisions “a priori” irrationnelles mais salvatrice.”
@Le Minarchiste
“Sans vouloir me vanter, je ne me fais pratiquement jamais berner par ces paradoxes et biais cognitifs.”
Et pourtant tu acceptes l’idée d’un pouvoir absolu et limité à la fois 😉
Le problème de Monty Hall est extrêmement intéressant et invite à se méfier des “évidences.”
J’en ai aussi parlé dans un article “vacances” de mon blog, de façon moins “savante” (voir le casse-tête de la fin) et Contrepoints l’avait d’ailleurs publié :
https://leblogdenathaliemp.com/2015/07/12/cinq-enigmes-et-un-casse-tete-pour-le-week-end-du-14-juillet/
Selon Wikipedia il semble que plusieurs réponses sont possibles si on ne précise pas (comme ici) suffisamment le protocole.
Wikipedia : Problème de Monty Hall, extrait :
“Que le présentateur ne peut ouvrir la porte choisie par le candidat.”
(…)
“Or, comme ces éléments n’étaient pas mis en avant dans l’énoncé du problème, et ce même s’ils étaient implicites, d’autres résultats statistiques que ceux donnés dans l’article devenaient possibles.”
“Selon Wikipedia il semble que plusieurs réponses sont possibles …”
Cela montre les limites de Wikipedia : si autant de personnes qui “croient” savoir ou sont de mauvaise foi que de personnes qui savent modifient les articles, la probabilité d’y rencontrer la vérité est de 50%. D’ici peu, on pourra y lire que le cheval blanc d’Henri IV était gris !
+1
gris clair ou gris foncé ?
peu importe Wikipedia
Ce qui m’a troublé lors de la lecture de l’article est justement le fait de savoir si le présentateur pouvait ou pas ouvrir la porte choisie par le candidat ? J’ai retrouvé cette interrogation sur Wikipedia c’est tout.
Cette information n’est pas anodine, elle est pourtant absente du protocole décrit par le Minarchiste.
Dans ces conditions, deux réponses sont possibles.
Extrait de l’article :
“Puis, Monty Hall ouvre l’une des deux autres portes derrière laquelle il sait qu’il y a une chèvre (disons la porte numéro 2).”
Autres !
Proba conditionnelles inverses. On ne cherche pas à savoir la proba au départ avec MH mais on part sur l’arrivé. Quelle est la proba d’avoir B sachant que l’événement A est réalisé. On raisonne sur l’arrivée et non sur le départ. Si on prend deux événements indépendants, c’est 50/50.
Si on raisonne en cherchant B sachant que A est réalisé, c’est 33/67
La meilleur explication est sur Wikipédia.
“Si l’on demande une réponse rapide et intuitive, deux points de vue incompatibles s’opposent.
– Le premier affirme qu’après ouverture de la porte, il reste deux portes, chacune ayant tout autant de chances de cacher la voiture. On a donc tout autant de chances de gagner avec changement que sans changement.
– Le second affirme que si l’on ne change pas de porte, on gagne si et seulement si on avait fait le bon choix au départ. Or, ce choix avait une chance sur trois d’être bon. Il y a donc 1/3 de chances de gagner sans changer, 2/3 de chances de gagner en changeant.”
Je ne suis pas d’accord, ça n’est pas une question d’intuition mais d’obstination, je crois qu’on appelle ça “biais de confirmation”. Ce que l’esprit a du mal à admettre, c’est que la décision de changer va obliger à renoncer à un gain possible qui résultait de la décision initiale, indépendamment de savoir si dans la nouvelle configuration on peut gagner plus facilement. Une fois une décision prise, on ne veut voir que ce qui semble en confirmer le bien-fondé. On a choisi une porte au hasard, on constate que ça n’était pas la mauvaise, donc on prend ça comme une confirmation de la justesse du premier choix. On a décidé de construire un ralentisseur, un automobiliste en excès de vitesse s’envole dessus et fauche une gamine pourtant bien sage sur le trottoir, on y voit une justification du ralentisseur…
Le biais de confirmation c’est plutôt persister dans l’erreur face à un problème et ce en recherchant des informations ou des raisonnements confirmant le choix initial.
Il y a 2 liens dans l’article : l’un sur l’aversion à la dépossession et l’autre sur le statu quo qui semblent plus proche de la raison qui nous conduit à faire le mauvais choix.
Mais force est de constater que certains commentateurs ici sont bien dans le biais de confirmation que vous décrivez quand ils insistent sur des points remettant en cause l’énoncé pourtant très clair, genre : “oui mais si l’animateur ne sait pas” ou “oui mais pour la foudre il faudrait tenir compte d’autres paramètres”.
Bon, perso je me suis bien marrer dans ce débat, c’est le principal… c’est mon biais à moi !
Ne reste plus qu’à apprendre à rire de soi pour commencer à réaliser la magie et la beauté de la vie.
Ca m’arrive de m’esclaffer “quel con!” en parlant de moi, n’ayez crainte…
Il me semble que votre second point de vue, Jean, est erroné. Le choix initial se fait avec une probabilité de 1/3. L’information apportée supprime une possibilité ( la présence de la voiture en porte 2) et réduit l’incertitude. De 3 les possibilités de réussite passe à 2.Compte tenu de l’information nouvelle, la probabilité de votre choix passe à 1/2 et les deux possibilités restantes sont équiprobables. Par nature l’information réduit l’incertitude (objective : pas forcément le sentiment d’incertitude) … c’est d’ailleurs par ce truchement que Claude Shannon a pu proposer “une mesure de l’information”
@simon: sauf que l’information ne concerne que les portes 2&3. La probabilité sur la porte 1 ne change pas. L’alternative au premier choix (2/3) ne repose plus que sur une seule porte, la 3!
L’être humain ne peut être rationnel, vu que la rationalité n’existe pas dans la nature, mais existe uniquement via le langage.
Dans la réalité, il n’existe pas de système fermé étant soumis à aucune condition préalable, ni de replicabilité parfaite.
C’est l’exemple de la foudre : mathématiquement l’auteur a raison, mais physiquement il a tort : la foudre répond à des lois qui font que la statistique est inapplicable : la foudre en se déclenchant change les conditions de déclenchement de la foudre suivante.
Je pense contrairement à l’auteur, que cette irrationnalité est une force, parce qu’elle permet de s’adapter et de décider : ce n’est pas grave d’avoir tort ou d’avoir raison, l’important c’est le résultat.
La raison est un outil, pas une nécessité.
“cette irrationnalité est une force”
Cette irrationalité peut prendre 2 formes :
– une approximation grossière pour prendre des décisions rapidement et rejeter le doute : l’instinct et l’intuition. On voit d’ailleurs combien il est difficile pour chacun d’admettre que son intuition le trompe.
– un biais “programmé” : l’individu n’a pas (ou faiblement) la notion d’espèce – au plus une conscience de groupe. Il est logique que l’intérêt individuel soit “trompé” pour maximiser l’intérêt de l’espèce (même au détriment du groupe). La plupart des réactions émotives sont irrationnelles. Mais au delà de certaines évidences, il est difficile de dire jusqu’où va cette irrationalité et même d’en prendre conscience et accepter cet état de fait.
Question idiote : L’énigme part du principe que l’animateur sait quelle porte ne pas ouvrir, mais si au lieu de ça l’animateur ouvrait n’importe quelle porte sans que lui-même ait connaissance de ce qui se trouve derrière, ça change la réponse?
Alors une fois sur trois le jeu est fini et il faut trouver un programme de remplacement.
L’animateur va ouvrir un garage et il faut trouver un autre animateur.
Oui, si l’animateur ne sait pas ce qui se trouve derrière la porte qu’il ouvre, cela change la réponse. On reviens sur du 50/50 pour les deux portes restantes.
En effet, ça n’est pas un problème de statistiques et de probabilités, mais d’information. Une fois les chèvres et la voiture disposées, la probabilité ne change pas, elle est passée de 1/3 partout à 1 pour la bonne porte et à 0 pour les autres. Ce qui change, c’est l’information que le candidat a sur cette probabilité. En ouvrant une porte (et pas au hasard !), l’animateur est forcé de donner une partie de l’information dont il dispose. Dans le cas où le candidat a choisi une porte chèvre (2 fois sur 3), l’animateur est contraint de choisir l’autre porte chèvre et donc implicitement de révéler la porte gagnante. En changeant son choix, le candidat est sûr de gagner s’il avait fait le mauvais au départ (2 fois sur 3) et sûr de perdre s’il avait fait le bon au départ (1 fois sur 3).
Merci pour vos réponses
Quelques explications qui m’ont semblé claires :
http://cortecs.org/materiel/solution-le-jeu-des-trois-boites-ou-probleme-de-monty-hall/
Totalement contre intuitif ce truc.
Ceci dit, la solution semble pouvoir se démontrer, et pas simplement d’argumenter…
il me semble qu un moyen facile de comprendre cet apparent paradoxe est de penser refaire l experience 2x 1000 fois.
Dans le premier c as vous garder 1000 fois votre choix et vous aller gagner 333 fois (approximatievement)
Dans le 2e cas vous changez systematiquement votre choix et vous aller gagtner 500 fois.
Et donc vous comprenez que changer systematiquement ameliore votre proba de gain.
Ou ai je rate qqchose ?
Cordialement
Larry
Vous pourrez ainsi constater, mais pas comprendre. Je doute d’ailleurs que la production de l’émission vous permette ces 1000 participations ! En fait, tout est dans les mots : changer systématiquement n’ “améliore” pas votre probabilité de gain, cela échange vos chances de gain contre vos chances de perte. C’est comme si d’un coup de baguette magique vous transformiez les voitures en chèvres et réciproquement. Refuseriez vous de le faire ?
Pour ceux qui n’ont pas compris, cela ne change rien que les nouvelles proba soit 50/50. Lors de votre choix vous aviez 33% de chance de trouver la voiture. Quand le présentateur ouvre l’autre porte, il vous informe qu’il ne reste plus que votre choix, et le bon choix, votre choix à été fait avec une probabilité de 33%, le nouveau choix avec une probabilité de 50%. Votre nouveau choix est donc plus probable d’être le bon que le premier.
“…cela ne change rien que les nouvelles proba soit 50/50.”
Pour un nouvel arrivant elles seraient de 50/50, pas pour vous puisque le choix de l’animateur a été fait en fonction du vôtre.
“Quand le présentateur ouvre l’autre porte, il vous informe qu’il ne reste plus que votre choix, et le bon choix, votre choix à été fait avec une probabilité de 33%, le nouveau choix avec une probabilité de 50%.”
“il ne reste plus que votre choix, et le bon choix…” : non, il reste juste 2 portes, votre choix initial pouvant d’ailleurs être le bon choix.
Non pas 50% mais 67%. Avec 100 portes on aurait 1/100 en restant sur le choix initial et 99/100 en changeant.
“Pour un nouvel arrivant elles seraient de 50/50, pas pour vous puisque le choix de l’animateur a été fait en fonction du vôtre.”
C’est cela dont je parlais dans “les nouvelles proba”. Parce que l’erreur est de prendre les deux situations séparément, ce que font les gens qui s’énerve sur ce fil.
C’est pourtant simple : pour gagner sans changer, il faut avoir choisi la bonne porte dès le début. Pour gagner en changeant, il suffit d’avoir choisi une mauvaise porte au départ.
Excellent !
Avocat du diable :
Suite à votre choix initial, vous serez d’accord avec moi que la voiture a 33% de chance d’être derrière la porte numéro 3 que vous n’avez pas choisie et 67% de chances d’être derrière l’une des deux autres portes (1 ou 2). Cependant, une fois que la porte numéro 2 est éliminée, cela signifie que la voiture a 67% de chance d’être derrière la porte numéro 1 ! Vous devriez donc choisir cette porte puisqu’elle a deux fois plus de chances de cacher la voiture !
Pour bien comprendre ce paradoxe apparent il faut réaliser que l’animateur sait ou se trouve les trois lots. Il n’ouvre donc pas une porte au hasard.
L’animateur élimine une porte perdante parmi les deux que le joueur n’a pas choisies. Comme il y a deux chances sur trois que le lot gagnant se trouve derrière ces deux portes l’animateur fournit un renseignement supplémentaire au joueur. Le raisonnement ne tient pas avec les portes 1 et 2 puisque l’animateur ne peut pas ouvrir la porte 1. Il n’y a donc pas élimination d’incertitude entre les portes 1 et 2.
Excellent ! C’est ce que tentent un peu vainement certains commentateurs de mettre en avant lorsqu’ils remettent en question l’action d’ouvrir la porte 2.
Ce geste est forcément calculé et vise évidemment une chèvre. Cette nouvelle information implique de redéfinir le problème.
Pourquoi le raisonnement simple suivant serait-il faux ?
Deux personnes choisissent chacun une porte. La troisième est alors ouverte qui cachait une chèvre. Si chaque personne modifie son choix initial, les deux auraient alors chacune 2/3 de chances. Ce qui est impossible…
Remplacez 3 portes par 100.
Il me semble que ce n’est pas une affaire de nombre : 100 ou 10 000 portes, c’est le même raisonnement, le nombre ajoutant simplement un côté spectaculaire censé convaincre, mais qui ne prouve rien.
Autre chose : je trouve que l’auteur passe trop vite sur la vérification expérimentale. J’aurais aimé qu’il détaille, incrédule que je suis, son protocole.
Ah, H16, quel plaisir de vous lire tous les jours ! Quelles tranches de rigolade, mais aussi de fulminations intérieures ! Je ne le dis pas à mon cardiologue, sinon il m’interdirait de vous lire !
Linarès, parce que déjà il faudrait savoir si les 2 joueurs peuvent choisir la même porte. S’ils ne peuvent pas, alors le choix du 2ème joueur est biaisé. Et si les 2 joueurs ne peuvent pas choisir la même porte alors la seule porte restante pour l’animateur serait une voiture et non une chèvre et le jeu serait fini.
Ca change fortement les probabilités.
Le coup des 67 % miraculeux ne parvient pas à me convaincre, même après avoir bien relu tous les commentaires ci-dessus. Car enfin, d’un point de vue strictement matériel, lorsque le « mage » ouvre une porte avec une bestiole derrière, rien ne change derrière les deux autres portes. L’opération mentale, artificielle, extérieure, consistant pour le joueur à modifier alors son choix initial ne peut rien changer non plus.
En réalité, puisque le joueur sait dès le début que le mage va obligatoirement supprimer une mauvaise porte, il a d’emblée une chance sur deux et certainement pas une sur trois.
Enfin, je crois…
Et merci bien à l’auteur de l’article pour la prise de tête !
Exactement, il y a 33 % de chance qu’elle soit derrière une des porte. lorsque l’une d’elle est ouverte ça fait du 50/50. a priori.
Ben non.
désolé mais votre raisonnement est impossible, la personne A choisit la porte A, la personne B choisit la porte B et la voiture se trouve derrière la porte C, le présentateur devrait ouvrir la porte B pour la A mais il devrait ouvrir la porte A pour la B, votre raisonnement ne tient pas la route. Est ce que vous vous avez finalement compris ou toujours pas?
Je ne suis pas en accord avec cette théorie, je regrette mais c’est faux. ET je vous explique le pourquoi ci dessous:
Soit ”x” le symbole qui represente qu’on ne sait pas ce qu’il y a derrière la porte.
Il y a deux chèvres et voiture en totale derrières les trois portes
1er cas:
Porte1 Porte 2 Porte3
x x x
Pour faire son choix, la probabilité de faire le bon choix et de gagner la voiture est = 1/3 = 0,33 = 33,33% (Peu importe la porte qu’on choisit).
Faisons le choix de la porte1 comme sur la video.
2eme cas: le présentateur nous revele ce qui se trouve derrière la porte3 (Une chèvre).
Porte1 Porte 2 Porte3
x x chevre
Si on arrive au milieu du jeu, c’est a dire qu’on doit faire notre choix pour la première fois en ayant comme donnes le 2eme cas, donc la probabilité de gagner la voiture serait = 1/2 = 0,5 = 50%.
Mais vu qu’on a deja fait le choix pour la porte1 en sachant que la probabilité était de 1/3, a ce moment la, notre chance de gagner continue a être 1/3 vu qu’on a deja fait notre choix. Par contre, en vu d’actualiser les calculs, vu qu’il est tres tres important, suivant la pensée latérale, d’imaginer tout ces algorithmes en fonction du temps. Sinon ce n’est plus de la mathématique, ca devient sophisme.
Donc en vue d’actualiser les calculs pour le sujet qui fait son choix, au moment ou il sait que une des deux chèvres se trouve derrière la porte3, il continue a avoir 1/3 de chances de gagner et 2/3 de perdre.
C’est a partir du moment ou le présentateur lui offre la possibilité de changer de choix, qu’il peut considérer que accepter ou refuser, je répète, accepter ou refuser implique que maintenant la probabilité de ganger est de 1/2. pas avant l’offre de changement. Donc il doit faire un choix, je répète le verbe devoir…pour vous expliquer un peu comment fonctionne l’univers dans ce sens, rien ne change, tout suit une courbe predeterminee, jusqu’a le moment ou on doit choisir, pas avant.
Si le sujet decide de ne pas changer, donc c’est 1/2 de gagner, l’offre du présentateur a augmente ces probabilités, pas la révélation.
Si le sujet decide de changer de choix, c’est a dire de se décider pour la porte2 au lieu de la porte1. Il aura 1/2 chance de gagner. pas 2/3.
Attention!
le premier choix est du a 100% au hazard, avec 1/3 chances de gagner.
Tout est relatif, n’oublions pas la leçon de Einstein. Ce problème mathématique ou ce dilemme nous mène toujours quelles que soient les décisions prises en compte, ou le moment d’arrivée en fonction du temps (debut ou milieu) a 2 seules resultas possibles : ”Gagner” ou ”Ne pas gagner” la voiture . Il n’existe pas la possibilité de gagner 2 chèvres par exemple…
Donc le changement de choix n’augmenterait en aucun cas les chances de gagner, vu que si on a fait le bon choix la 1ere fois, changer de choix serait un mauvais choix y viceversa.
Donc le résultat final serait:
1/3 pour le 1er cas
le 2eme cas se composerait de deux possibilités en fonction du moment d’arrivée (Debut ou milieu).
Debut = 1/3
Milieu = 1/2
Et le dernier cas, ou on nous offre changer de choix en sachant que la porte3 contient une chèvre serait toujours = 1/2 peu importe le premier choix dans le 1er cas vu au 100% de hazard ajoute a formule 1er cas.
Donc la formule 3eme cas continue a porter le ”100% de hazard” sinon il s’agirait d’une formule simplifiée. Donc imprécise et qui donnerait un 2/3 en cas de s’être décide pour le changement.
Quant a l’option de faire la meme opération plusieurs fois pour prouver votre théorie, je la met en doute et je me justifie avec ceci:
Si on fait la même opération 1 million de fois par exemple, et qu’on determine que la probabilité de changer de choix donne de meilleures résultats que de garder son choix. Ce ne serait pas concluant a moins qu’on puisse refaire l’opération 1 million de fois plusieurs fois.
Et même ainsi, il faudrait aussi tenir en compte la somme de toutes les fois qu’on a realize l’opération 1 million de fois. Ceci pourrait tout changer, parceque la conclusion pourrait être interessante du moins du point de vue de la science de la turbulence. Vu qu’il pourrait avoir des coïncidences tres surprenantes et même inquietantes.
Merci pour cette article.
Salutations
Comme plusieurs ici, je me suis fait avoir par le paradoxe de Monty Hall. Et j’ai fini de comprendre la source de mon erreur : Elle vient paradoxalement de mon effort d’analyser au mieux l’énoncé.
Après lecture, J’ai considéré les 3 portes sous la forme d’un ensemble composé de 2 sous ensembles : le premier pour le choix du candidat, avec un singleton ; le second avec les 2 autres portes restantes.
Quand le présentateur supprima une porte, il restait – pour moi – 2 portes avec forcément 2 chances identiques.
Mon erreur vient du fait que j’ai confondu les sous ensembles avec leur élément singleton !
En réalité, ce sont les sous ensembles qui portent les probabilités, et les conservent après l’intervention du présentateur !
Je reprends :
– après choix du candidat, on a : le sous ensemble A avec 1 chance /3 de contenir la voiture, le sous ensemble B avec 2/3 (le complément)
– retrait de la porte “chèvre” de l’ensemble B
– les probabilité sur les ensembles restent identiques, sauf que l’élément restant de B se retrouve avec une probabilité de 2/3 !
Finalement, je préfère cette solution plutôt que modifier l’énoncé avec 50 ou 1milliard de portes. J’ai un faible pour la théorie des ensembles 😉
Oui, mais ce n’est un sous-ensemble qu’on nous demande choisir, mais une porte…
Pensez à des numéros dans 2 sacs… L’important est de distinguer l’impact du retrait d’une porte sur la probabilité des autres.
Manifestement je suis un indécrottable idiot ! L’information apportée (présence d’une chèvre en porte 2) fait simplement passer la probabilité de l’événement souhaité (présence de la voiture en porte 1) de 1/3 à 1/2 : la probabilité d’un événement n’a rien à voir avec l’idée que l’on s’en fait a priori … Dans ce cas une possibilité a été éliminée, il n’en reste plus que deux a priori (compte tenu des informations données) équiprobables.
Décidément non. Testez avec 100 portes au lieu de 3.
@Simon: Non.
Imaginons que vous avez 2 sacs pour mettre les numéros des portes, respectivement “mon premier choix” et “les autres choix”.
Au premier tour, vous mettez 1 dans le sac MPC, et les 2 et 3 dans LAC.
Pour le premier sac, vous avez 1/3 d’avoir raison et par conséquent, 2/3 pour le second sac.
Maintenant, si vous supprimez le numéro 2 du second sac, croyez vous encore que:
– le premier sac devient plus probable ?
– le second sac devient moins probable ?
– ou que le numero restant dans le second sac prend pour lui toute la probabilité ?
Bonjour,
Sans doute suis-je incompétent mais je ne comprends pas son problème.
Après le 1er tirage, on dévoile la porte 2.
Il reste donc 2 portes et on fait un second tirage avec 50% pour chaque porte.
87% des gens ne changent pas et ils ont raisons :
L’idée que le fait qu’une porte soit dévoilée a comme conséquence que la probabilité devient 66% et 34 est stupide et révèle une méconnaissance des probabilités. Les tirages n’ont pas de mémoire et on passe à 50/50 et pas 66/34 au 2ème tirage.
Ceci dit quand bien même on passerait à 66/34 qui dit que ce n’est pas le 1er choix qui a 66% ???
Si quelqu’un peut m’expliquer !!
87% des gens ont du bon sens : changer au risque de perdre provoquera plus de regrets que persister.
C’est mon avis
@jlduret:
Pour un second tirage à 50%, il faudrait qu’on réaffecte au hasard les numéros 1 et 3 aux portes restantes.
Relisez les précédents commentaires.
@jlduret
Comme dit à de multiples reprises mais ça commence à etre un peu touffu les commentaires :
– Choisissez une porte parmi 100 (chaque porte a donc un chance sur 100 d’avoir la voiture)
– Je vous ouvre les 98 autres portes (toutes donc sauf la vôtre et une autre)
– La voiture a 99 chances sur 100 d’être derrière cette autre porte et la vôtre n’a toujours q’une chance sur 100
Si vous ne percevez pas intuitivement là que les chances des 98 portes se sont transférés uniquement sur celle que je n’ai pas ouverte exprès…
Je suis très étonné de constater comment on peut aussi facilement adhérer à ce genre de raisonnement complètement faux!…
Lorsque le présentateur ouvre la porte No 2, il donne une solution au problème qui du coup n’est plus le même. Les probablités sont remises à zero et le problème n’est plus le même. Donc à partir de ce moment là les calculs repartent à zero et c’est du 50-50.
Vos démonstrations sont complètement fausses… De cette manière on peut aussi ´prouver’ que l’homme n’a jamais marché sur la Lune… Et ainsi de suite…