Par Nathalie MP

Les énoncés des cinq énigmes du 14 juillet se trouvent dans l’article 5 énigmes et un casse-tête pour le week-end du 14 juillet. Voici les solutions.
Solutions des définitions de mots croisés :
1. ENTRACTE
Tristan Bernard “Remplit les lavabos et vide les baignoires” (huit lettres)
2. INTERNATIONALE
Robert Scipion “Tube de rouge” (quatorze lettres)
3. ORSAY
Michel Laclos “Gare à la peinture” (cinq lettres)
4. INSTITUTRICES
Michel Laclos “Des maîtresses pas toujours chéries” (treize lettres)
5. BECASSINE
Michel Laclos “Une bonne partie du Finistère” (neuf lettres)
Première énigme : Les pièces de monnaie
Il suffit de prélever au hasard 10 pièces et de les retourner. Cela fonctionne comme un charme dans tous les cas :
– Les dix pièces prélevées sont Face. On les retourne, elle deviennent Pile. On a bien 10 pièces Pile de chaque côté.
– On a prélevé 9 pièces Face et 1 pièce Pile. On les retourne et on obtient 9 pièces Pile dans le nouveau lot, comme dans le lot d’origine qui vient de perdre une pièce Pile.
– On a prélevé 8 pièces Face et 2 pièces Pile. On les retourne et on obtient 8 pièces Pile dans le nouveau lot, comme dans le lot d’origine qui vient de perdre 2 pièces Pile.
Etc… jusqu’à :
– On a prélevé par hasard les 10 pièces Pile. On les retourne et on obtient un lot de 10 pièces Face. Il n’y a pas de pièce Pile dans ce lot, comme dans le lot d’origine qui vient de se voir amputé de toutes ses pièces Pile.
Deuxième énigme : La bouteille
Appelons X le volume du liquide restant dans la bouteille. X = 495,45 ml.
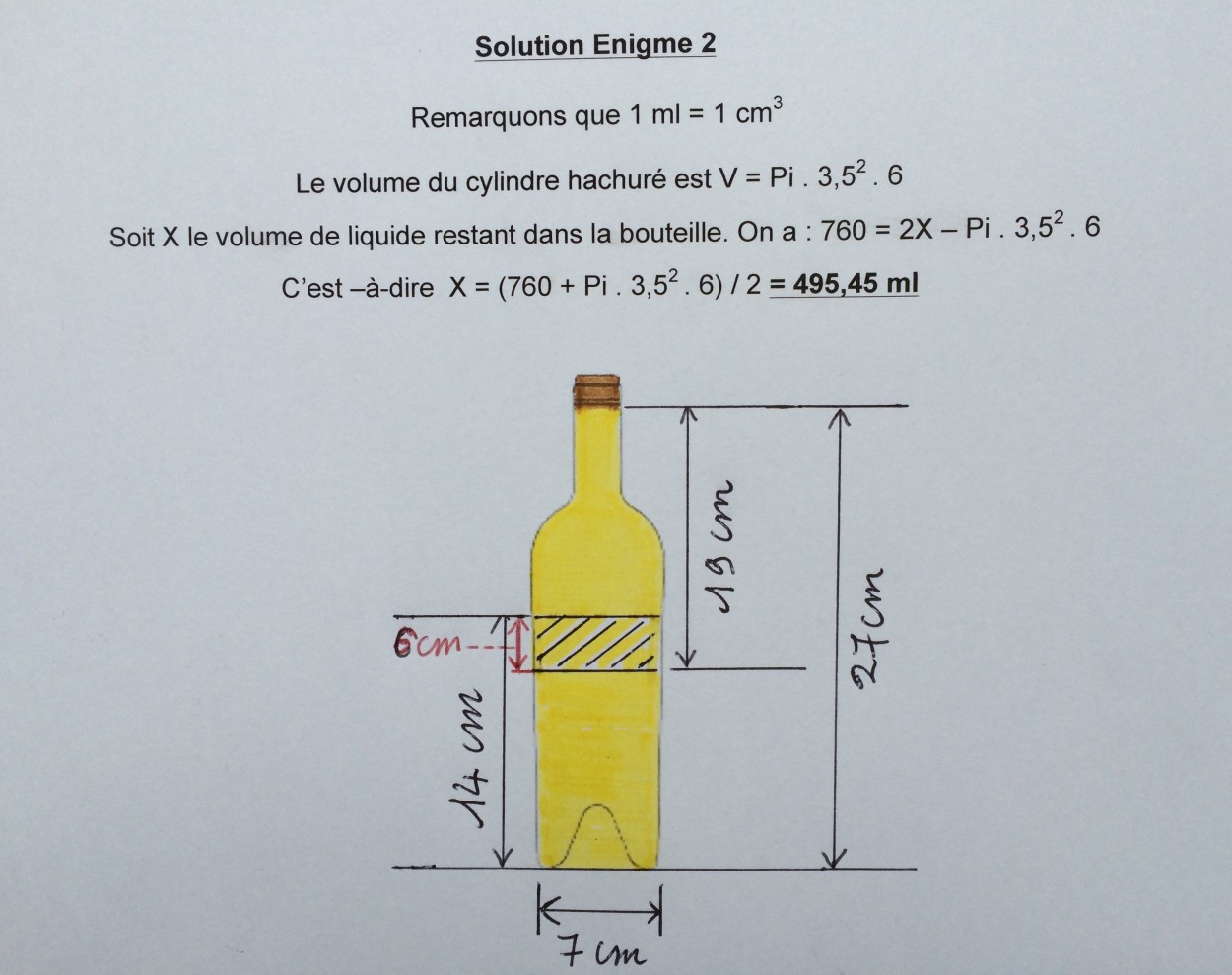
Pour arriver à ce résultat, superposons les deux positions de la bouteille données dans l’énoncé. On constate que dans cette situation imaginaire, la bouteille est non seulement pleine mais débordante : en effet, elle contient deux fois X et donc le volume hachuré sur le schéma ci-contre est compté deux fois. Pour obtenir les 760 ml qui correspondent au volume de la bouteille pleine, il faut donc retrancher 1 fois le volume hachuré.
Rappelons que 1 cm3 = 1 ml. Le volume hachuré V est un cylindre de hauteur 6 cm (= 14 + 19 – 27) et de rayon 3,5 cm (= 7 cm / 2). V = π . 3,52 . 6
Le volume de la bouteille pleine est donc : 760 = 2X – V = 2X – π . 3,52 . 6
Il s’ensuit que X = (760 + π . 3,52 . 6) / 2 = 495,45 ml (arrondi au centième).
Troisième énigme : Les âges des trois filles
Solution : Les trois filles de Dodo la Finance ont 9 ans, 2 ans et 2 ans.
Information 1 : Le produit des trois âges est égal à 36.
Il n’y a que huit combinaisons possibles :
1 x 1 x 36 – 1 x 6 x 6 – 2 x 3 x 6 – 2 x 2 x 9 – 4 x 3 x 3 – 1 x 2 x 18 – 1 x 3 x 12 – 1 x 4 x 9
Information 2 : La somme des trois âges est égale au numéro de la maison d’en face.
Dans le même ordre que ci-dessus, les sommes des âges sont :
38 – 13 – 11 – 13 – 10 – 21 – 16 – 14
Comme Arnaud Montebourg, qui vient de faire les mêmes calculs que nous, ne peut pas donner de réponse à ce stade, on en déduit que le numéro de la maison d’en face est le 13 qui apparait deux fois dans nos huit sommes. Les âges des trois filles sont donc soit (6 ans, 6 ans et 1 an) soit (9 ans, 2 ans et 2 ans).
Information 3 : L’aînée a les yeux bleus.
Cette information nous indique qu’il y a une seule aînée et pas des jumelles aînées. On en déduit que la bonne combinaison d’âges est : 9 ans, 2 ans et 2 ans.

Quatrième énigme : Le paradoxe de la deuxième fille
Solution : La probabilité que l’autre enfant soit aussi une fille est de 1/3.
Information 1 : Dans la famille d’Arnaud Montebourg, il y a deux enfants.
Les combinaisons possibles en tenant compte du rang de naissance sont :
Fille Garçon – Fille Fille – Garçon Fille – Garçon Garçon
Information 2 : La lecture de Paris Match vous apprend que l’un est une fille.
On peut donc éliminer la combinaison Garçon Garçon. Il reste trois combinaisons, dont une seule sur les trois correspond à la situation voulue, c’est à dire la combinaison Fille Fille. La probabilité que l’autre enfant soit aussi une fille est donc de 1/3.
Cinquième énigme : Devinette pour aller au paradis
La question à poser à chacun des deux hommes est : “D’après vous, quelle porte m’indiquera votre compagnon si je lui demande de me montrer la porte du paradis ?”
- Si vous la posez au menteur, il vous montrera la porte qui mène à l’enfer, car il sait que son compagnon, qui ne ment jamais, montrera la porte du paradis. Comme lui ment, il va indiquer la porte de l’enfer.
- Si vous la posez à l’homme qui ne ment jamais, il vous montrera aussi la porte qui mène à l’enfer car il sait que son compagnon qui ment toujours montrera la porte de l’enfer et non la porte du paradis.
En conséquence, vous savez quelle est la porte qui mène à l’enfer et il ne vous reste plus qu’à emprunter l’autre pour atteindre le paradis.
+ Casse-Tête : Las Vegas 21 ou le problème de Monty Hall
La solution a déjà été donnée dans l’article d’origine : Ben a intérêt à changer de choix car il passe ainsi d’une probabilité de gain de 1/3 à 2/3.
L’article de Wikipédia que j’avais cité en lien indique différentes méthodes pour arriver à ce résultat de 2/3 : arbres de décision, calcul par les probabilités de Bayes. Pour mieux “visualiser” ce résultat peu intuitif, on peut aussi se reporter à cette page consacrée au paradoxe de Monty Hall.





Plus simple, on prend toutes les pièces et on n’en retourne aucune.
“Quatrième énigme : Le paradoxe de la deuxième fille”
Pas d’accord avec la réponse: la probabilité est de 1/2, et non 1/3.
On n’a pas le droit de simplement supprimer le cas “garçon-garçon” et de supposer que, par défaut, les trois restants sont équiprobables. Car le cas “fille-garçon” est valable seulement si la fille est l’aînée, et le cas “garçon-fille” seulement si c’est la cadette; en revanche, le cas “fille-fille” compte double:
Car si la fille dont il est question est l’aînée, on a le choix entre “fille-fille” et “fille-garçon”, avec une probabilité de 1/2 pour chaque; et si la fille est la cadette, on a le choix entre “fille-fille” et “garçon-fille”, avec une probabilité de 1/2 pour chaque.
On ignore si la fille est l’aînée ou la cadette, mais on sait à coup sûr qu’elle est forcément soit l’une, soit l’autre. Donc dans les deux cas possibles, la réponse est 1/2.
Il y a donc en réalité quatre cas:
“La fille est l’aînée et elle a un frère cadet”, “La fille est l’aînée et elle a une sœur cadette” // “La fille est la cadette et elle a un frère aîné”, “La fille est la cadette et elle a une sœur aînée”.
Deux de ces quatre cas correspondent à la configuration “fille-fille”.
L’erreur provient du fait que, lorque vous passez de quatre cas à trois en éliminant garçon-garçon, vous supposez arbitrairement que les trois cas restants sont également probables, ce qui est faux.
Impossible d’éditer les commentaires, alors je résume:
Tant qu’on ignore le sexe des enfants, quatre cas équiprobables:
G-G = 1/4 || G-F = 1/4 || F-G = 1/4 || F-F = 1/4
Quand on apprend l’existence d’une fille, la probabilité de G-G passe à zéro, et se redistribue sur les trois autres cas. Vous pensez à tort que l’opération est triviale et consiste à redistribuer également:
G-G = 0 || G-F = 1/3 || F-G = 1/3 || F-F = 1/3
Ce que je pense avoir montré, c’est que vous avez en réalité désormais le choix entre quatre cas dont deux correspondent à F-F:
G-G = 0 || G-F = 1/4 || F-G = 1/4 || F-F = 1/2
Je pense aussi que la probabilité est de 1/2. En effet, en la matière, la présence d’un autre enfant n’a aucune influence sur cette probabilité, qui est biologiquement de 1/2, quel que soit le nombre d’enfants déjà présents…
Humm..
En genetique si vous avez un gene recessif qui est lethal in utero s’il est homozygote, vous aurez:
DomRec RecDom DomDom RecRec(léthal donc pas de naissance)
Le risque d’avoir un enfant vivant est bien 1/3 1/3 1/3.
Ps je me méfie les statistiques c’est piègeant 🙂
Ce n’est pas la présence de l’autre enfant qui fait changer les probabilités.
Si le problème nous disait que l’ainée est une fille alors la probabilité que la cadette le soit aussi serait bien de 1/2.
Par contre, l’information est seulement que l’une des deux est une fille, on a donc 2 chances sur trois d’être dans une configuration fille-garçon (ou garçon-fille) qui est deux fois plus probable qu’une configuration fille-fille.
Réponse à propos de la 4ème énigme “le paradoxe de la 2è fille” :
Ca s’appelle paradoxe car c’est contre-intuitif et là aussi il faut que le problème soit bien posé. Des variantes peuvent amener des résultats différents.
Pb : dans cette famille il y a 2 enfants. je vous apprends que l’un est une fille. Quelle est la proba que l’autre soit une fille ?
Soit A l’événement “l’autre est aussi une fille”
Soit B l’événement “Un des enfants est une fille”
On cherche P (A) sachant B
P(A) sachant B = P(A et B) / P(B)
P(A et B) = 1/4 (probabilité que l’un et l’autre soient des filles)
P(B) = 3/4 (probabilité que l’un est une fille (sur 2 enfants : c’est comme lancer une pièce deux fois de suite)
Donc P(A) sachant B = 1/4 * 4/3 = 1/3
De quoi débattre ici : http://villemin.gerard.free.fr/Wwwgvmm/Probabil/Famille.htm#soeurs
Ce n’est un paradoxe que parce que la façon de formuler la question est fautive. En réalité, la probabilité P(B) est de 1/2. Quand vous prenez un des enfants au hasard, il y a une chance sur deux que ce soit un garçon, et une chance sur deux que ce soit une fille, puisque vous ignorez a priori le sexe des enfants. La probabilité dont il est question est bien que “cet enfant-là” soit une fille, et non que n’importe lequel des deux enfants soit une fille.
Donc P(A) sachant B = P(A et B) / P(B) = (1/4)/(1/2) = 1/2
Puisque vous mentionnez le lancer de pièces, imaginez la situation suivante:
Pendant que vous tournez le dos, je tire à pile ou face avec deux pièces sur une table, puis j’en recouvre une sous une surface opaque. Vous vous retournez, et vous pouvez voir une des pièces, qui est tombée sur pile. Quelles sont les chances que l’autre soit aussi tombée sur pile? Elles sont évidemment de 1/2, parce qu’on calcule la probabilité “sachant que” la pièce visible est tombée sur pile (et elle avait une chance sur deux de le faire, indépendamment du nombre de pièces), et non “sachant que” au moins une pièce sur les deux est tombée sur pile (proba de 3/4, qui dépend du nombre de pièces lancées).
Remplacez “pièce visible” et “pièce invisible” par “enfant connu” et “enfant inconnu”, et vous obtenez le même résultat.
Ce que vous décrivez ne correspond pas à l’énigme.
On sait que l’un des enfants est une fille mais pas lequel. cela correspond à un lancé de deux pièce ou vous m’annoncez qu’une pièce est pile mais sans que je sache laquelle.
Dans ce cas là, la seule information que je peux en tirer c’est que les deux pièces ne sont pas face et que je suis donc face à une configuration pile-face, face-pile ou pile-pile (avec 1/3 pour chaque configuration).
“On sait que l’un des enfants est une fille mais pas lequel.”
L’enfant connu est une fille, peu importe que ce soit l’aînée ou la cadette.
Si l’enfant connu est l’aînée, il y a 1 chance sur 2 que la cadette soit une fille.
Si l’enfant connu est la cadette, il y a 1 chance sur 2 que l’aînée soit une fille.
Or l’enfant connu est nécessairement soit l’aînée, soit la cadette.
Donc il y a soit 1 chance sur 2, soit 1 chance sur 2.
Vous n’avez pas besoin de savoir “quelle” pièce est pile pour savoir qu’il y a une chance sur deux pour que l’autre soit pile, et une chance sur deux pour qu’elle soit face. Cette chance est indépendante du résultat de l’autre pièce, et du nombre de pièces lancées.
Conclusion: il y a 1 chance sur 2.
La phrase “Conclusion: il y a 1 chance sur 2” précède le dernier paragraphe sur les pièces.
(L’absence de possibilité d’éditer est décidément agaçante.)
J’ajouterai que dans l’analogie des pièces, vous ne savez pas laquelle a été tirée en premier, donc c’est strictement la même chose que pour les enfants. La question de l’ordre n’a aucune importance, et le sophisme consiste justement à faire comme si elle en avait. Que vous voyiez la pièce de vos yeux ou que je vous donne verbalement le résultat d’une des deux, ça revient au même.
Vous répondez à une autre énigme. Passez à 1000 tirages. J’ai tiré à pile ou face 1000 fois et je vous dis que j’ai obtenu 999 fois pile n’est pas du tout la même chose que de vous laisser voir 999 pièces sans les choisir et que vous constatiez qu’elles sont toutes sur pile.
Si vous aviez l’information que l’ainée est une fille alors il y’aurait bien 1 chance sur 2 que la cadette soit aussi une fille (et vice versa si la cadette est une fille). Seulement, ce n’est pas l’information que vous avez.
L’information qui dit que l’un des enfants est une fille est équivalente à “ce ne sont pas tous les deux des garçons”.
“Si l’enfant connu est l’aînée, il y a 1 chance sur 2 que la cadette soit une fille.
Si l’enfant connu est la cadette, il y a 1 chance sur 2 que l’aînée soit une fille.”
En faisant ce raisonnement, vous comptez la probabilité fille-fille deux fois.
Si l’aînée est une fille, il y a 1 chance sur 2 que le cadet soit un garçon, 1 chance sur 4 que la cadette soit une fille et que Match parle de l’ainée et 1 chance sur 4 que la cadette soit une fille et que match parle de la cadette.
Si la cadette est une fille, il y a 1 chance sur 2 que l’ainé soit un garçon, 1 chance sur 4 que l’ainée soit une fille et que Match parle de l’ainée et 1 chance sur 4 que l’ainée soit une fille et que match parle de la cadette.
Si l’enfant connu est la cadette, il y a 1 chance sur 2 que l’aînée soit une fille.
Les cas ou les deux sont des filles se retrouvent deux fois.
“Si l’aînée est une fille, il y a 1 chance sur 2 que le cadet soit un garçon, “, OK
“1 chance sur 4 que la cadette soit une fille et que Match parle de l’ainée et 1 chance sur 4 que la cadette soit une fille et que match parle de la cadette.” NON.
Vous introduisez une hypothèse supplémentaire qui n’est pas dans l’énoncé : que si les deux enfants sont une fille Paris-Match choisi de parler de l’une ou de l’autre avec une probabilité 1/2, et si c’est un garçon il n’en sera pas parlé. Alors que l’énoncé dit que Paris-Match a parlé d’un enfant (avec une probabilité de 1 !) pas de l’autre.
“ainé” est une caractéristique qui permet de distingue les deux enfants, mais il y en pleins d’autres possible : roux, fan de tennis, ou … “dont le sexe est indiqué par Paris-Match” (ci après : SP pour “sexe publié”) !
Remplacez “ainé” par “SP”, et cadet par “NSP” dans vos calcul et cela donne :
“Si SP est une fille, il y a 1 chance sur 2 que NSP soit un garçon, 1 chance sur 4 que la NSP soit une fille et que Match parle de SP et 1 chance sur 4 que la NCP soit une fille et que match parle de NSP. ” Ce qui est évidemment faux : par définition, Match parle de SP, pas de NSP. la probablité que Match parle de NSP est NULLE, pas 1/4, et réciproquement la probabilité que NSP soit une fille et que Match parle de SP est de 2/4, pas 1/4.
la formulation correcte est donc simplement “SP est une fille, il y a 1 chance sur 2 que NSP soit un garçon (et 2 chance sur 4 que la NSP soit une fille et que Match parle de SP) ”
Et la suite ?
“Si NSP est une fille, il y a 1 chance sur 2 que SP soit un garçon” : NON , l’énoncé précise que SP n’est pas un garçon. c’ets pas 1/2 mais zéro
” 1 chance sur 4 que SP soit une fille et que Match parle de SP”. non, par définition c’est 1, pas 1/4
” et 1 chance sur 4 que SP soit une fille et que match parle de NSP”. non, c’est zéro. Match parle de SP ,jamais de NSP.
comme le fait remarquer Pmn votre analogie est incorrecte car on ne sait pas quelle pièce est pile.
L’énoncé correct serait, un individu tire à pile ou face deux pièces et dit au joueur qu’il y a une des pièces qui est pile. Il lui demande ensuite s’il parie sur face ou pile pour l’autre pièce. Il n’y a pas à hésiter, il faut parier sur face.
Une explication intuitive. Imaginons qu’on effectue 4000 double-lancers. On aura grosso modo 1000 lancers Pile/Pile, 1000 Face/Face et 2000 Pile/Face (ou Face/Pile). A chaque fois qu’on a Face/Face, le jeu est annulé, pas de paris, on rejoue. Sur les 3000 lancers (environ) où le joueur joue, il aura intérêt à parier sur Face car il y a aura grosso modo 2 fois plus de lancers où il gagnera. Ce qui correspond bien à une probabilité de 1/3 pour pile.
On a là un cas saisissant de probabilité subjective, bayesienne. La probabilité exprime ici un degré de connaissance ou de méconnaissance.
“L’énoncé correct serait, un individu tire à pile ou face deux pièces et dit au joueur qu’il y a une des pièces qui est pile. Il lui demande ensuite s’il parie sur face ou pile pour l’autre pièce. Il n’y a pas à hésiter, il faut parier sur face. ”
mais si, il faut hésiter.
* vous ne savez pas si la pièce est lestée ou pas. Si elle est lestée, le fait qu’elle soit sorti pile une fois augmente les chances que les autres tirages soient piles eux aussi et il vaut mieux parier “pile”.
* vous ne savez pas si “l’animateur” (appelons -le comme ça puisque c’est une situation “Monty Hall”) a choisit une pièce au hasard, puis indiqué qu’elle était “pile”, ou si il a cherché une pièce pile
* et si il a choisit pile, vous ne savez pas si il l’a fait dans l’ensemble minoritaire ou dans l’ensemble majoritaire.
Au final je choisirais de parier Pile, en partant du principe que l’animateur a choisit dans l’ensemble le plus fréquent.
On en revient à Monty Hall, sauf que dans Monty Hall il y a une hypothèse explicite qui manque ici : l’animateur choisit spécifiquement une porte PARCE qu’elle est perdante, et vous le savez.
– je suis d’accord avec votre première critique. Il est vrai que le fait que les pièces sont bien équilibrées est nécessaire.
– Par contre, concernant votre deuxième remarque, je ne suis pas d’accord. je précise bien que l’animateur tire les pièces à pile ou face et dit s’il y a une pièce tombée sur pile ou non. Si c’est non je jeu s’arrête et on recommence. Il ne cherche rien.
– Concernant votre dernière remarque, j’avoue que je ne sais pas trop quoi répondre. Qu’appelez-vous ensemble majoritaire et ensemble minoritaire ? L’animateur n’a rien à choisir il dit seulement au joueur s’il y a un pile et lui demande de parier sur l’autre pièce.
Le paradoxe ne tient pas, selon moi, seulement à un problème de formulation. C’est un problème d’information. Imaginons que les deux pièces soient discernables par exemple une pièce euro et une pièce dollar. Au lieu de dire qu’une des pièces est tombée sur pile, l’animateur lui annonce que c’est la pièce dollar qui est tombée sur pile, le joueur a une information supplémentaire ce qui change la probabilité. Par contre lorsqu’il lui annonce qu’une des pièces est tombée sur pile, il dispose de moins d’informations, ce qui change la probabilité par rapport au cas d’avant.
En fait, dans l’énoncé originel (les filles), ce qui provoque le paradoxe c’est à la fois la formulation mais également la conception qu’on a de la probabilité. Lorsqu’on conçoit la probabilité seulement comme objective (une loi naturelle), c’est certain que cela pose problème. Mais une probabilité provient de la combinaison entre une loi naturelle et les informations dont disposent les individus.
Exemple : un devin qui donne la bonne réponse à tous les coups vous dit que le prochain tirage à pile ou face donnera pile. La probabilité que la pièce tombe sur pile, si vous savez que le devin ne se trompe jamais sera de 1. Et pourtant cela ne signifie pas que la pièce tombera sur pile à tous les coups, la probabilité restera de 1/2.
oui, c’est bien une question d’information et donc la formulation est cruciale (et, dans le cas de l’énigme telle qu’elle est posée ici, insuffisante)
la question est simple : le fait de savoir qu’une pièce est pile vous renseigne-t-il sur l’autre pièce ?
c’est oui si, et seulement si, le choix de la première (celle qui est annoncée) dépend de l’état de la second
c’est non dans le cas contraire.
Dire qu’il y a un pile c’est bien un choix. le processus étant
1) parmi les pièce qui n’ont pas encore été regardées, en choisir une selon une méthode M
2) la regarder ; si la pièce est pile, l’annoncer. fin.
3) sinon, si toutes les pièces n’ont pas été examiné, recommencer en 1)
4) fin. (l’énoncé n’est pas clair en cas d’absence de pièce pile, mais il n’est de toute façon intéressant que si il y a une pièce pile, quitte à recommencer le tirage jusqu’à ce que cela arrive)
dans ce processus, la méthode M est absolument cruciale. Si on a pré-ordonné les pièces, ou si on les tire au hasard (ce qui revient strictement au même), le choix de la pièce NE dépend évidemment PAS des pièces qui n’ont pas encore été examinées et le fait qu’on est trouvé un “pile” ne renseigne en rien sur l’état des suivantes (seul le fait d’annoncer qu’il n’y a pas de pile renseigne sur le fait qu’il n’y a que des faces)
Le vice c’est qu’il y d’autres méthodes, et notamment on peut trier les pièces (c’est ce qui se passe dans “Monty Hall” ), auquel cas évidemment l’état des pièces suivantes et l’état de la pièce annoncé ne sont pas indépendants, et l’état de celle annoncé donne un renseignement … mais seulement à celui qui sait comment le tri a été fait !
notez que “trier les pièces” ça revient à faire une annonce relative à un tirage pipé comme si il avait été fait avec une pièce truquée (le tirage en lui même ne l’est pas, truqué, c’est l’annonce qui l’est). Ce tirage truqué ne nous renseigne pas sur le “vrai” tirage. Autrement dit savoir que la pièce annoncé est “pile” ne nous apprend rien, à moins de connaitre la méthode de trucage.
L’intention de l’énigme est clairement de nous faire aboutir à la conclusion “paradoxale” que la probabilité que l’autre enfant soit aussi une fille n’est que de 1/3.
Malheureusement, je suis d’accord avec Y33Sha : la formulation “La lecture de Paris Match vous apprend que l’un est une fille.” ne permet pas, en toute rigueur, de tirer cette conclusion.
elle est fautive parce qu’elle autorise deux interprétations différentes :
A) un enfant s’est présenté par hasard. Paris-Match en parle et en précise le sexe : féminin. Cela ne dit évidemment RIEN sur le sexe de l’autre enfant, qui reste M/F avec une probabilité 1/2 !
B) parmi les enfants, il y en a dont Paris-Match parle PARCE QUE c’est une fille. Aucun hasard, c’est un choix délibéré. On a enlevé un F du pool des sexes possible pour l’enfant restant, et la probabilité F tombe de 2/4 à 1/3 .
Par définition du hasard, “série causale indépendante”, on aurait été dans le cas A si on avait parler de l’enfant ainé … mais aussi bien de l’enfant cadet, roux, handicapé, gaucher, fan de tennis, habillé en rouge, le premier arrivé, penché à la fenêtre, ou n’importe quelle caractéristique distinguant cet enfant de l’autre dont le sexe est en question : la précision complémentaire “Paris Match n’a pas dit que cette fille était l’aînée” ne suffit pas à exclure, en toute rigueur, cette interprétation. Cette précision a même un effet pervers : “l’enfant dont Paris-Match indique le sexe” est tout aussi caractéristique que “l’enfant né le premier = l’ainé”. L’indication censée nous orienter vers le cas B nous oriente en fait vers le cas A.
Bref, le paradoxe ne réside que dans l’ambiguïté de la formulation initiale…
Je préfère ma solution pour l’énigme 5 :
* un homme, et a fortiori deux, ne restent pas devant la porte du paradis sans y entrer s’il savent l’identifier et l’ouvrir. Donc ce n’est pas la peine de leur demander “D’après vous, quelle porte m’indiquera votre compagnon si je lui demande de me montrer la porte du paradis ?” : il ne connaissent pas la réponse, ou la porte est bloquée.
* devant le paradis sans pouvoir entrer ? ces deux hommes vivent l’enfer.
* si ils sont en enfer, et qu’il y a une porte qui y “mène”, c’est que cette porte est à sens unique et qu’on est du coté de la sortie. La porte du paradis est donc la seule qui peut s’ouvrir. Mais il y a une autre condition, sans quoi les deux hommes aurait ouvert par hasard et ne seraient plus là.
* Une des voies vers le paradis, c’est d’avoir des actions positives à l’égard de tous, aussi pêcheur soit-il. La situation ne permet pas d’autres actions que poser une question. Cette question doit refléter le souhait que tout le monde accède au Paradis.
solution : demander aux hommes “voulez vous venir avec moi au Paradis ?” (par exemple )
La porte de l’enfer restera fermée (elle est à sens unique, mais dans l’autre sens) ; celle du paradis sera celle qui pourra s’ouvrir, et vous pourrez passer avec les deux hommes