Les vacances, qui pour beaucoup commencent ce week-end, sont synonymes de détente et de liberté, mais elles signifient aussi parfois longs trajets en train ou en avion, attentes interminables dans les aéroports ou longs moments un peu rasoirs sur la plage. Dans ces cas-là, il y a d’abord la solution des gazettes plus ou moins people, puis celle des cahiers de sudoku. Si l’on se sent la fibre plus littéraire, on ira volontiers vers le roman policier à suspens ou les mots croisés plein d’esprit. À ce propos, je ne résiste pas au plaisir de rappeler quelques définitions aussi célèbres qu’astucieuses
Tristan Bernard : « Remplit les lavabos et vide les baignoires » (huit lettres)
Robert Scipion : « Tube de rouge » (quatorze lettres)
Michel Laclos : « Gare à la peinture » (cinq lettres)
Michel Laclos : « Des maîtresses pas toujours chéries » (treize lettres)
Michel Laclos : « Une bonne partie du Finistère » (neuf lettres)
Si l’on se sent d’humeur à la fois batailleuse et badine, on lira avec originalité et décontraction le Petit traité d’anti-écologie de H16. Et si, en plus, on aime les chiffres et les défis logiques, un monde d’énigmes et de casse-têtes nous tend les bras. En voici cinq, complétés par la présentation d’un problème de probabilité très connu et toujours très discuté car fortement contre-intuitif.
Première énigme : pièces de monnaie
100 pièces de monnaie sont posées les unes à côté des autres sur une table. Les conditions sont telles que vous ne pouvez pas les voir et que vous ne pouvez pas reconnaître au toucher si elles présentent le côté pile ou le côté face. Parmi ces 100 pièces, vous savez que 10 montrent le côté pile et 90 montrent le côté face, mais vous ne savez pas lesquelles.
On vous demande de prélever à l’aveuglette parmi les 100 pièces le nombre x de pièces qui permettra de créer in fine un second lot qui comportera autant de pièces pile que le premier lot, lequel sera donc diminué de x pièces. Le total de pièces présentes sur la table reste 100.
Questions : comment procéder et combien vaut x ?
Remarque : toutes les manipulations sont possibles (plonger les pièces dans l’huile bouillante, les peindre en rouge, etc…) sauf, comme je l’ai dit, reconnaître par la vue ou le toucher la qualité pile ou face des 100 pièces de la situation initiale.
.Deuxième énigme : bouteille
 Voici une bouteille de Loupiac de forme classique : le fond est légèrement bombé vers l’intérieur et le col dans lequel s’insère le bouchon est progressivement plus étroit que le corps de la bouteille. Sa contenance du fond jusqu’à la base du bouchon est de 760 ml et sa hauteur de la surface de la table à la base du bouchon est de 27 cm. Le diamètre intérieur du cylindre formant le corps est de 7 cm. On néglige l’épaisseur du verre.
Voici une bouteille de Loupiac de forme classique : le fond est légèrement bombé vers l’intérieur et le col dans lequel s’insère le bouchon est progressivement plus étroit que le corps de la bouteille. Sa contenance du fond jusqu’à la base du bouchon est de 760 ml et sa hauteur de la surface de la table à la base du bouchon est de 27 cm. Le diamètre intérieur du cylindre formant le corps est de 7 cm. On néglige l’épaisseur du verre.
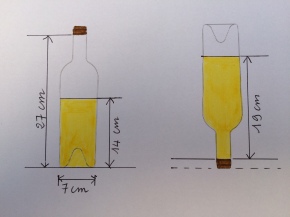 Comme on vient tout juste de prendre l’apéro, la bouteille n’est plus très pleine. Posée normalement sur la table, la hauteur de liquide restant en partant du fond est de 14 cm. Si on la retourne, c’est-à-dire si on la pose sur le bouchon, la hauteur de vin restant à partir de la base du bouchon est de 19 cm, comme le montre le schéma ci-contre.
Comme on vient tout juste de prendre l’apéro, la bouteille n’est plus très pleine. Posée normalement sur la table, la hauteur de liquide restant en partant du fond est de 14 cm. Si on la retourne, c’est-à-dire si on la pose sur le bouchon, la hauteur de vin restant à partir de la base du bouchon est de 19 cm, comme le montre le schéma ci-contre.
Question : quel est le volume de Loupiac restant dans la bouteille ? Donner le résultat en ml, arrondi au centième.
Remarque : une calculette peut être utile, sauf si on sait multiplier π de tête avec n’importe quel nombre.
Troisième énigme : les âges des trois filles
Arnaud Montebourg rencontre son ami Dodo la Finance qu’il n’a pas vu depuis longtemps. Celui-ci lui annonce qu’il a maintenant trois filles. Faisant preuve d’un intérêt poli, Arnaud lui demande leurs âges respectifs. Dodo répond que le produit des trois âges est égal à 36.
Arnaud, toujours très fort en calcul, on a vu ça quand il était ministre, rétorque immédiatement que cette information ne lui permet pas de déterminer les âges des trois filles. Dodo ajoute alors que la somme des trois âges est égale au numéro de la maison d’en face.
Jetant un rapide coup d’œil au numéro en question et calculant à toute vitesse dans sa tête, Arnaud persiste à dire qu’il manque d’information. Dodo lui précise que l’aînée a les yeux bleus. Et d’un seul coup, tout devient clair pour Arnaud.
Question : quels sont les âges des trois filles de Dodo la Finance ?
Remarque : contrairement à ce que la présence d’Arnaud Montebourg pourrait laisser croire, ce problème n’est pas aussi farfelu qu’il en a l’air. Indice : exploiter les informations les unes après les autres.
Quatrième énigme : le paradoxe de la deuxième fille
Dans la famille d’Arnaud Montebourg, il y a deux enfants. La lecture de Paris Match vous apprend que l’un est une fille.
Question : quelle est la probabilité que l’autre soit aussi une fille ?
Indice : Paris Match n’a pas dit que cette fille était l’aînée.
Cinquième énigme : devinette pour aller au paradis
Vous êtes face à deux portes. L’une s’ouvre sur l’enfer et l’autre sur le paradis, mais vous ne savez pas laquelle mène au paradis et laquelle mène à l’enfer.
Deux hommes sont présents à côté de ces portes. L’un est toujours menteur, l’autre dit toujours la vérité.
Vous ne pouvez poser qu’une seule et même question aux deux hommes pour savoir quelle porte prendre pour aller au paradis.
Question : quelle est cette question ?
Remarque : une seule question, la même à chacun des deux hommes.
.+ le casse-tête : Las Vegas 21 ou le problème de Monty Hall
Las Vegas 21 est un film de Robert Luketic dans lequel Ben (Jim Sturgess), un étudiant du MIT extrêmement doué pour les mathématiques, est repéré par son professeur (Kevin Spacey) après avoir résolu avec succès le délicat problème de probabilité connu sous le nom de Monty Hall. Suite à cela, il va intégrer l’équipe de blackjack montée par le professeur avec d’autres élèves très brillants afin de gagner la somme d’argent nécessaire pour payer sa scolarité.
Dans la vidéo ci-dessous (2′ 20″) voici l’exposé du problème de Monty Hall tel que présenté dans le film par Kevin Spacey, ainsi que la bonne réponse :
Ce problème reprend un jeu télévisé qui était animé par un certain Monty Hall, d’où son nom. Ben est confronté à trois portes, qu’on nommera portes 1, 2 et 3. Il doit en choisir une parmi elles. Il sait que derrière l’une des portes se trouve une Ferrari, et que derrière chacune des deux autres se trouve une chèvre.
À ce moment du jeu, la probabilité que la Ferrari se trouve derrière la porte 1, ou derrière la porte 2, ou derrière la porte 3 est égale dans les trois cas à 1/3. Mettons que Ben choisisse la porte 1. Jusque-là tout va bien.
Mais à ce point du jeu, l’animateur, qui sait exactement où sont les chèvres et où est la Ferrari, ouvre la porte 3 dans le cadre de laquelle on découvre une chèvre. On en déduit que la Ferrari se trouve derrière la porte 1 ou la porte 2, et idem pour la deuxième chèvre. L’animateur demande alors à Ben s’il désire modifier son choix.
Dans l’extrait de Las Vegas 21 ci-dessus, Ben répond qu’il veut changer de porte. Le professeur le met en garde : comme l’animateur sait où est la Ferrari, sa question sur le changement de choix vise peut-être à influencer le candidat pour qu’il perde. Ben répond que son changement de choix est uniquement motivé par les probabilités. Alors qu’il avait 1/3 de chance de gagner la Ferrari quand il a choisi la porte 1 en début de jeu, il a maintenant 2/3 de chance de la gagner en changeant de choix, et en allant donc vers la porte 2.
Question : pourquoi ? Expliquez le raisonnement de Ben.
Important : le présentateur connait exactement la disposition derrière les portes. Il n’ouvre pas les portes au hasard. Il n’ouvre pas la porte choisie initialement par Ben et il ouvre forcément une porte montrant une chèvre.
La réaction intuitive consiste à dire que maintenant que l’animateur a ouvert la porte 3 montrant une chèvre, il y a autant de chance que la Ferrari soit derrière la porte 1 que derrière la porte 2. Un changement de choix n’améliore donc pas la situation du candidat dont les chances de gain sont de 1/2. C’est la solution qui m’est venue d’abord à l’esprit, mais elle est inexacte.
Le bon résultat, contre-intuitif mais confirmé par de nombreux tirages par ordinateur, correspond à une probabilité de Bayes (probabilité d’un événement sachant que…) et considère que si on ne change pas de porte, on garde la probabilité initiale de gagner la Ferrari, soit 1/3, tandis que si l’on décide de changer de porte, on atteint la probabilité de 1 – 1/3 = 2/3.
Une part importante de la controverse de Monty Hall résulte de la façon de poser le problème en spécifiant plus ou moins bien les choix possibles du présentateur lorsqu’il ouvre une porte montrant une chèvre. L’ensemble des thèses qui s’affrontent sont exposées dans cet article de Wikipédia. Je vous laisse méditer. Bon 14 juillet à tous !
- Toutes les réponses aux énigmes et au casse-tête le samedi 18 juillet sur le site de Nathalie MP !





Bonjour
Le premier est facile, merci google 🙂
Je dirais qu’en choisissant x=20 et en tirant les 20 pièces à pile ou face, je devrais statistiquement avoir 10 piles. Mais ça me paraît trop con pour être ça.
Quoique après avoir relu le problème, je dirais qu’il faut choisir 50 pièces au hasard.
non, il y’a une méthode pour réussir à coup sur sans rien laisser au hasard et aux probas.
Une fois que l’on s’est rendu compte qu’il n’y’a qu’une seule action possible à faire sur ces pièces qui ait du sens, la solution est assez facile à trouver.
Merci pour l’indice, j’ai trouvé moi aussi.
l’indice final “toutes les manipulations sont possibles” est de trop, en fait c’est pas un indice, c’est carrément la solution.
L’intérêt de ces énigmes est de nous montrer que même quand on a une information parfaite on n’est pas capable de prendre la bonne décision !
Pour la première énigme il manque une information on ne sait pas si chacune des pièces à un coté pile et un côté face. Si chaque pièce possède un côté pile et un côté face la solution est évidente sinon il n’y en a pas.
Une énigme supplémentaire :
10 sacs contiennent chacun 100 pièces toutes identiques. mais dans un sac, les pièces sont fausses.
On dispose d’une balance. On sait que les vraies pièces pèsent 2g et les fausses 1g.
Comment déterminer dans quel sac se trouve les fausses pièces en n’effectuant qu’une seule pesée ?
C’est fastoche, le sac avec des pièces d’euro grecque contient les fausses pièces.
Et le sac contenant des Euros-PQ français n’est pas de meilleur aloi 🙂
La balance donne le poids exact ou bien seulement penche vers le plateau le plus lourd ?
Si la balance donne le poids exact, j’ai une solution.
Pareil. on pèse en même temps un nombre de pièces différent de chaque sac.
Une balance par définition comporte deux plateaux et l’on s’en sert généralement pour obtenir la masse en équilibrant les deux plateaux.
On appelle à tort balance des instruments qui sont des dynamomètres comme le pèse personne qui en fait mesure la force exercée par un corps et affiche une masse grace à relation la relation P=m*g
Ca ne répond pas à ma question.
Une balance à deux plateau peut permettre d’indiquer la masse exacte si j’ai des masses marquées à ma disposition ou bien seulement d’indiquer le plateau le plus lourd.
Ca ne change rien au problème d’un coté du plateau vous mettez une pièce du premier sac 2 du deuxième et ainsi de suite jusqu’au dixième et de l’autre de l’autre vous mettez 55 pièces provenant du même sac dit témoin.
Si la masse de vos 55 pièces provenant des différents sac est supérieure à la masse des pièces provenant du sac témoin votre sac témoin est celui qui contient les fausses pièces.
Sinon vous savez que votre sac témoin contient des vrais pièces qui font 2 g et qu’en fonction du nombre que vous en ajouterez pour équilibrer la balance vous trouverez le numéro du sac contenant des fausses pièces.
Le truc, c’est que ajouter des masses pour équilibrer la balance fait partie d’une seule pesée, utiliser des pièces pour le même rôle reviens à faire plusieurs pesées, ce qui est contraire à l’énoncé.
C’est bien cette solution que j’avais en tête. Par contre, il n’y a que 45 pièces à mettre sur un plateau de la balance, le dixième sac étant votre sac témoin.
Si pour vous équilibrer une balance à deux plateaux c’est une seule pesée, alors le fait d’utiliser des masses de 2g appelées pièces pour trouver ou dépasser cet équilibre ne devrait pas vous gêner.
Il est vrai que prendre les pièces des sac de 1 à 9 est suffisant pour déterminer le quel contient les fausses pièces, mais en prenant des pièces des sacs de 1 à 10 et 55 pièces d’un sac témoins ça marche aussi mais ça demande un peu plus d’effort.
la balance donne le poids exact. la fait de jouer avec les mots ne change pas grand chose, si vous prenez une balance Roberval ne change pas grand chose. Il suffit d’ajouter comme données le fait que vous disposez de poids de 2g et de 1g en illimité.
Indice : avec Antonov, la balance majore le poids de 100%…
Elle donne le poids exact.
Non une balance ça mesure une masse.
Le poids c’est une force qui s’exprime en Newton.
Si vous amenez votre pèse-personne sur la Lune vous allez vous trouver très maigre, alors que si vous y amenez une balance de Roberval elle vous donnera votre masse exacte.
bien entendu. Ici il s’agit d’abus de langage. je vous rappelle simplement qu’une masse ne peut se mesurer directement, même avec une balance de Roberval. Ce qu’on mesure avec une balance de Roberval c’est un équilibre entre deux forces, qu’on peut traduire via Newton par une égalité de masse.
Pour la deuxième énigme, je trouve 495.45 ml
Quelqu’un d’autre a trouvé la réponse ?
J’ai trouvé pareil.
Cinquième énigme : devinette pour aller au paradis
Moi, je ne demanderais pas à Antonov, car il me désignerait la mauvaise porte…
Je demanderais à chacun quelle porte va me désigner son collègue si je lui demande celle qui mène en enfer. Celui qui dit la vérité va m’indiquer le porte qui mène au paradis, puisque c’est celle que m’aurait montré le menteur. Le menteur me montrera aussi celle qui mène au paradis, car celui qui dit la vérité m’aurait indiqué celle qui mène en enfer, et comme le menteur ment…
Celui qui dit la vérité ment c’est gênant.
Non.La question, c’est pas quelle porte mène en enfer, c’est quelle porte son collègue me montre. Celui qui dit la vérité tient compte du mensonge de son collègue, s’il ne le faisait pas, il mentirait.
pour la 5ème énigme : on peut la résoudre très facilement si on est malin. Par exemple, poser la question suivante : si on ajoute 1 à 1, trouve-t-on 2 ?
Ce n’est pas ce genre de question qu’on attend dans l’énigme. Un indice : poser une question sur une question.
énigme 5 bis
Vous pouvez bien sûr traiter la 5ième énigme sur le mode logico-logique, comme fredd, et ça vous donnera une solution. Mais je vous propose de la prendre sur un mode théo-logique. Comme un Koan.
Je vous donne la solution : “voulez-vous me suivre vers le Paradis ?”
L’énigme 5 bis est de trouvez pourquoi
Indices, sous forme de questions préliminaires :
1) pourquoi deux hommes (des hommes ! pas des gardes, anges ni démons, ni des animateurs de jeu télé connaissant la solution et possédant déjà une Ferrari), devant des portes dont l’une ouvre sur le paradis, restent-ils dans cette situation ?
2) quel nom donneriez vous à la place où se trouvent ces deux hommes ?
3) quelle sorte d’action ouvre la voie vers le paradis ? et la ferme ?
1) Parce qu’ils n’ont ni bras ni jambes et qu’ils ne peuvent donc ni ouvrir ni suivre celui qui ouvre une porte.
2) Le purgatoire
3) La repentance
Solution de l’énigme des sacs de pièces :
Prendre 1 pièce dans le sac 1, 2 pièces dans le sac 2, 3 pièces dans le sac 3, etc, 10 pièces dans le sac 10 et peser.
En fonction de la mesure donnée par la balance on trouve où sont les fausses pièces. Par exemple, si le sac 1 contient les fausses pièces, on trouvera 109g, si c’est dans le sac 2, on trouvera 108, etc, si c’est dans le sac 10 on trouvera 100g